练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,在平面直角坐标系中,已知三个顶点的坐标分别是.

    (1)请在图中,画出绕着点逆时针旋转后得到的,则的正切值为 .

    (2)以点为位似中心,将缩小为原来的,得到,请在图中轴左侧,画出,若点是上的任意一点,则变换后的对应点的坐标是 .

    【答案】（1）图详见解析，；（2）图详见解析，变换后的对应点的坐标是.

    【解析】

    1）依据旋转的方向、角度和旋转中心，即可得到△ABC绕着点O逆时针旋转90°后得到的△A1B1C1，进而得到∠A1C1B1的正切值；.

    （2）依据点O为位似中心，将△ABC缩小为原来的，即可得到△A2B2C2，以及变换后的对应点P′的坐标．

    (1)如图所示,即为所求；由题可得，；

    (2)如图所示,即为所求，

    ∵点是上的任意一点，点为位似中心，

    ∴变换后的对应点的坐标是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校文体艺术节期间，举办“爱我云南，唱我云南”文艺晚会．每个班推荐一个节目参加晩会表演，参加晚会表演的节目均获奖，奖项分为一等奖、二等奖、三等奖和优秀奖，明明根据获奖情况绘制岀如图所示的两幅统计图．请你根据图中所给信息解答下列问题．

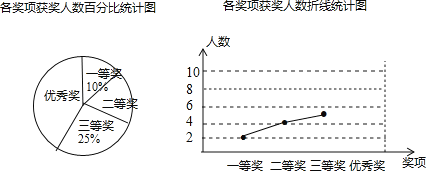
    （1）二等奖的获奖人数所占的百分比是　 ；

    （2）在此次比赛中，一共有多少同学参赛？请将折线统计图补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

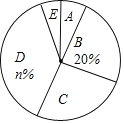
    【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中只选一类最喜爱的电视节目，以下是根据调查结果绘制的统计图表的一部分．

    类别

    A

    B

    C

    D

    E

    节目类型

    新闻

    体育

    动画

    娱乐

    戏曲

    人数

    12

    30

    m

    54

    9

    请你根据以上的信息，回答下列问题：

    （1）被调查的学生中，最喜爱体育节目的有　 　人，这些学生数占被调查总人数的百分比为　 　%．

    （2）被调查学生的总数为　 　人，统计表中m的值为　 　，统计图中n的值为　 　．

    （3）在统计图中，E类所对应扇形圆心角的度数为　 　．

    （4）该校共有2000名学生，根据调查结果，估计该校最喜爱新闻节目的学生数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上的A、B、C三点所表示的数分别为a、b、1，且|a﹣1|+|b﹣1|＝|a﹣b|，则下列选项中，满足A、B、C三点位置关系的数轴为（　　）

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

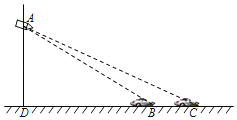
    【题目】如图，一辆轿车在经过某路口的感应线B和C处时，悬臂灯杆上的电子警察拍摄到两张照片，两感应线之间距离BC为6m，在感应线B、C两处测得电子警察A的仰角分别为∠ABD＝18°，∠ACD＝14°．求电子警察安装在悬臂灯杆上的高度AD的长．

    （参考数据：sin14°≈0.242，cos14°≈0.97，tan14°≈0.25，sin18°≈0.309，cos18°≈0.951，tan18°≈0.325）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

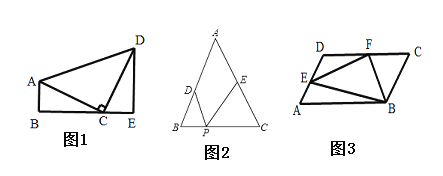
    【题目】（问题引入）

    如图（1），在中，，，过作则交延长线于点，则易得

    （直接应用）

    如图,已知等边的边长为,点, 分别在边, 上, , 为中点，为当上一动点，当在何处时，与相似，求的值.

    （拓展应用）

    已知在平行四边形中，，，，,，求长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】联想三角形外心的概念，我们可引入如下概念。

    定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心。

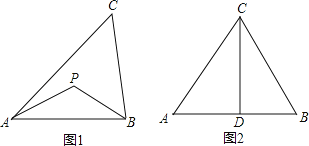
    举例：如图1，若PA=PB，则点P为△ABC的准外心。

    应用：如图2，CD为等边三角形ABC的高，准外心P在高CD上，且PD=AB，求∠APB的度数。

    探究：已知△ABC为直角三角形，斜边BC=5，AB=3，准外心P在AC边上，试探究PA的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

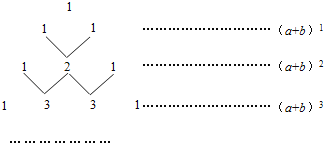
    【题目】我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左、右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2＝a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3＝a3+3a2b+3ab2+b2展开式中的系数等．

    （1）（a+b）n展开式中项数共有　 　项．

    （2）写出（a+b）5的展开式：（a+b）5＝　 　．

    （3）利用上面的规律计算：25﹣5×24+10×23﹣10×22+5×2﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的顶点坐标为A（﹣2，3），B（﹣3，2），C（﹣1，1）．

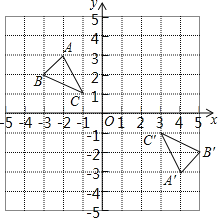
    （1）若将△ABC向右平移3个单位长度，再向上平移1个单位长度，请画出平移后的△A1B1C1；

    （2）画出△A1B1C1绕原点顺时针旋90°后得到 的△A2B2C2；

    （3）若△A′B′C′与△ABC是中心对称图形，则对称中心的坐标为 ．

    查看答案和解析>>

    同步练习册答案