
 (1)5.
(1)5.| 1 |
| 16 |
| 1 |
| 16 |


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
| 1 |
| 20 |
| 1 |
| 20 |
查看答案和解析>>
科目:初中数学 来源:2013年广东省广州市南沙区中考一模数学试卷(带解析) 题型:解答题
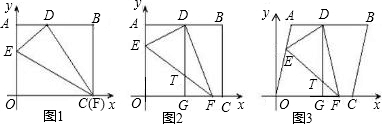
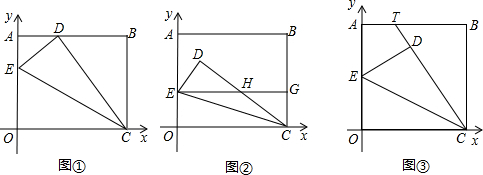
将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。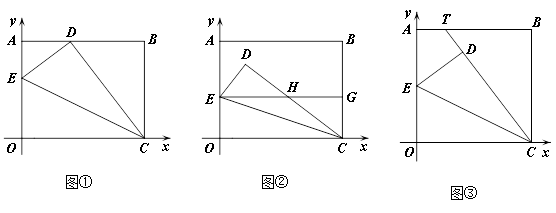
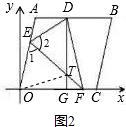
(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
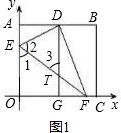
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥ 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;
(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
查看答案和解析>>
科目:初中数学 来源:2013年广东省广州市南沙区中考一模数学试卷(解析版) 题型:解答题
将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。

(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥ 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;
(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
查看答案和解析>>
科目:初中数学 来源:2009年北京市朝阳区中考数学二模试卷(解析版) 题型:解答题
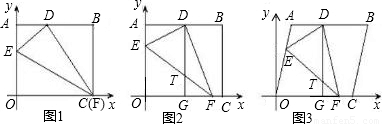
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com