
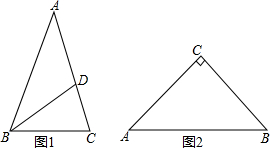
 我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形,若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.在Rt△ABC中,∠C=90°,AC=4,BC=3,E,F分别在边AC,BC上,且EF是△ABC的“内似线”,求EF的长.
我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形,若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.在Rt△ABC中,∠C=90°,AC=4,BC=3,E,F分别在边AC,BC上,且EF是△ABC的“内似线”,求EF的长. 分析 分两种情况:①当 $\frac{CE}{CF}$=$\frac{AC}{BC}$=$\frac{4}{3}$ 时,②当 $\frac{CF}{CE}$=$\frac{AC}{BC}$=$\frac{4}{3}$时,分别求解即可.
解答 解:解:设D是△ABC的内心,连接CD,
则CD平分∠ACB,
∵EF是△ABC的“內似线”,
∴△CEF与△ABC相似;
分两种情况:①当 $\frac{CE}{CF}$=$\frac{AC}{BC}$=$\frac{4}{3}$ 时,EF∥AB,
∵∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
作DN⊥BC于N,如图2所示:
则DN∥AC,DN是Rt△ABC的内切圆半径,
∴DN=$\frac{1}{2}$(AC+BC-AB)=1,
∵CD平分∠ACB,
∴$\frac{DE}{DF}$=$\frac{CE}{CF}$=$\frac{4}{3}$ (可以用面积法证明),
∵DN∥AC,
∴$\frac{DN}{CE}$=$\frac{DF}{EF}$=$\frac{3}{7}$,即 $\frac{1}{CE}$=$\frac{3}{7}$,
∴CE=$\frac{7}{3}$,
∵EF∥AB,
∴△CEF∽△CAB,
∴$\frac{EF}{AB}$=$\frac{CE}{AC}$,即 $\frac{EF}{5}$=$\frac{7}{3}$,
解得:EF=$\frac{35}{12}$;
②当 $\frac{CF}{CE}$=$\frac{AC}{BC}$=$\frac{4}{3}$时,同理得:EF=$\frac{35}{12}$;
综上所述,EF的长为 $\frac{35}{12}$.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、三角形的内心、勾股定理、直角三角形的内切圆半径等知识;本题综合性强,有一定难度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解某班学生最喜爱的体育项目 | B. | 核实某位病人血液中被感染的病毒 | ||
| C. | 了解长江中鱼的种类 | D. | 调查一批炮弹的杀伤半径 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
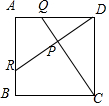 图中ABCD为正方形,Q及R分别为AD及AB上的点,DR与CQ相交于P,已知AQ=BR.
图中ABCD为正方形,Q及R分别为AD及AB上的点,DR与CQ相交于P,已知AQ=BR.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com