
【题目】解答
(1)如图1,小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系. 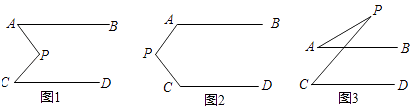
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A()
∵PQ∥AB,AB∥CD.
∴PQ∥CD()
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 .
(2)应用:
在图2中,若∠A=120°,∠C=140°,则∠APC的度数为;
(3)拓展:
在图3中,探索∠APC与∠A,∠C的数量关系,并说明理由.
【答案】
(1)两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;小明
(2)100°
(3)解:∠APC=∠C﹣∠A,
理由是:如图3,∵AB∥CD,
∴∠C=∠POB,
∵∠APC=∠POB﹣∠A,
∴∠APC=∠C﹣∠A
【解析】解:(1)如图1,过点P作PQ∥AB, 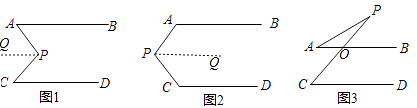
∴∠APQ=∠A(两直线平行,内错角相等),
∵PQ∥AB,AB∥CD,
∴PQ∥CD(平行于同一直线的两直线平行),
∴∠CPQ=∠C,
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C;
所以答案是:两直线平行,内错角相等,平行于同一条直线的两条直线互相平行,小明;
2)如图2,过P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠A+∠APQ=180°,∠C+∠CPQ=180°,
∵∠A=120°,∠C=140°,
∴∠APQ=60°,∠CPQ=40°,
∴∠APC=∠APQ+∠CPQ=100°,
所以答案是:100°;
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A. -a(a+1)=-a2+1 B. a(-a+1)=-a2-1
C. -x2(x-1)=x3+x2 D. (-x)2·(x-1)=x3-x2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求实数![]() 的取值范围;
的取值范围;
(2)0可能是方程一个根吗?若是,求出它的另一个根;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.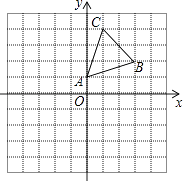
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1向左平移3个单位后得到△A2B2C2 , 画出△A2B2C2 , 并写出顶点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断下列几组选取样本的方法是否合适:
(1)小丽想了解某市中学生晚上在家复习功课的时间,调查了她所在学校九年级的50名同学;
(2)苗苗想了解她所在学校的学生课外阅读名著的情况,随机调查了该校50名同学;
(3)某电视台需要了解某个节目的收视率,对一所大学的学生进行了调查.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com