
���� ��1�����ݡ��任�㡱�Ķ����ɣ�
��2�������ֱ��l�Ϻ���������������ȵĵ�C��Ȼ���ҳ���A��B��C�ġ��任�㡱A�䡢B�䡢C�䣬��������C��A�䡢C��B�伴�ɣ�
��3������ͼ�Σ�������W������C���������C��B������ʱͼ��W���������㣬Ȼ��ֱ���⼴�ɣ�
���  �⣺��1����-2��3���ı任�������ǣ�-2��-3����
�⣺��1����-2��3���ı任�������ǣ�-2��-3����
��6��-1���ı任�������ǣ�-1��-6����
��2��ֱ��AB�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
x=yʱ��x=$\frac{4}{3}$��
���ԣ���C������Ϊ��$\frac{4}{3}$��$\frac{4}{3}$����
��C��ı任�������Ϊ��$\frac{4}{3}$��-$\frac{4}{3}$����
A�ı任�������Ϊ��0��-4����
B�ı任�������Ϊ��0��-2����
��ͼ˼·�����ɵ�A��B���������ֱ��l�Ľ���ʽ��
�����ֱ��l�Ϻ���������������ȵĵ�C���꣬������ı任��C������꣬
����ֱ��l�ϵ�C����ĵ�A��Bȷ�������ǵı任��A�䡢B�䣬
��������C��A�䡢C��B�䣬
����C��A���C��B����ɵ�ͼ�μ�Ϊ����
��3�������߾�����C��ʱ��-$\frac{4}{3}$=-$\frac{3}{4}$����$\frac{4}{3}$��2+c��
���c=0��
������������C��B������ʱ����ֱ��C��B�����ʽΪy=kx+b��
��$\left\{\begin{array}{l}{\frac{4}{3}k+b=-\frac{4}{3}}\\{b=-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$��
���ԣ�ֱ��C��B��Ľ���ʽΪy=$\frac{1}{2}$x-2��
����������������y�ã�-$\frac{3}{4}$x2+c=$\frac{1}{2}$x-2��
�����ã�3x2+2x-4c-8=0��
��=22-4��3��-4c-8��=0��
���c=-$\frac{25}{12}$��
����������c��ȡֵ��ΧΪc=-$\frac{25}{12}$��c=0��
���� ���⿼���˶��κ���ͼ���뼸�α任����Ҫ�����˴���ϵ������������ʽ����������ֱ�ߵĽ������⣬�����б�ʽ��������Ŀ��Ϣ�����⡰�任�㡱�Ķ����ǽ���Ĺؼ����ѵ����ڣ�3���жϳ���������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
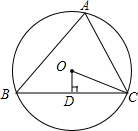 ��ͼ����ABC�ڽ��ڡ�O��OD��BC�ڵ�D������A=70�㣬���COD�Ĵ�СΪ70�㣨�ȣ���
��ͼ����ABC�ڽ��ڡ�O��OD��BC�ڵ�D������A=70�㣬���COD�Ĵ�СΪ70�㣨�ȣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
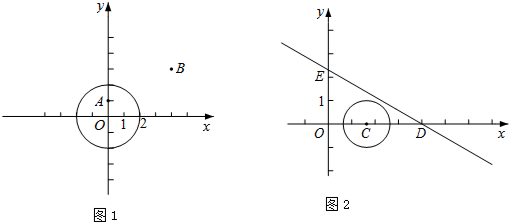
 ��ͼ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�ԲO1��O2��O3�������һ��ƽ�������ߣ���P��ԭ��O���������������������˶����ٶ�Ϊÿ��$\frac{��}{2}$����λ���ȣ����2017��ʱ����P�������ǣ�2017��1����
��ͼ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�ԲO1��O2��O3�������һ��ƽ�������ߣ���P��ԭ��O���������������������˶����ٶ�Ϊÿ��$\frac{��}{2}$����λ���ȣ����2017��ʱ����P�������ǣ�2017��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 264��103 | B�� | 2.64��104 | C�� | 2.64��105 | D�� | 0.264��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
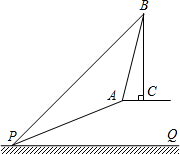 ��ͼ����֪б��AP���¶�Ϊi=1��$\sqrt{3}$���³�APΪ20m�����¶�A����ͬ-ˮƽ������-������BC����б�µ�P����ø���������B������Ϊ45�㣬���¶�A����ø���������B�����Ǧ���tan��=3����
��ͼ����֪б��AP���¶�Ϊi=1��$\sqrt{3}$���³�APΪ20m�����¶�A����ͬ-ˮƽ������-������BC����б�µ�P����ø���������B������Ϊ45�㣬���¶�A����ø���������B�����Ǧ���tan��=3�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com