
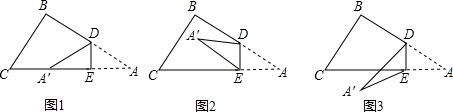
分析 翻折问题要在图形是找着相等的量.图1中DE为折痕,有∠A=∠DA′A,再利用外角的性质可得结论∠BDA′=2∠A图2中∠A与∠DA′E是相等的,再结合四边形的内角和及互补角的性质可得结论∠BDA′+∠CEA′=2∠A图3中由于折叠∠A与∠DA′E是相等的,再两次运用三角形外角的性质可得结论.
解答 解:(1)∠BDA′=2∠A;
故答案为:∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°
∴∠A+∠DA′E=360°-∠ADA′-∠A′EA
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°
∴∠BDA′+∠CEA′=360°-∠ADA′-∠A′EA
∴∠BDA′+∠CEA′=∠A+∠DA′E
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′-∠CEA′=2∠A
理由:DA′交AC于点F,
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′
∴∠BDA′=∠A+∠A′+∠CEA′
∴∠BDA′-∠CEA′=∠A+∠A′
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′-∠CEA′=2∠A.
点评 遇到折叠的问题,一定要找准相等的量,结合题目所给出的条件在图形上找出之间的联系则可.


科目:初中数学 来源: 题型:选择题
| A. | 4.8万元 | B. | 5.2万元 | C. | 5.4万元 | D. | 5.8万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )
如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )| A. | 1+$\sqrt{5}$或1+2$\sqrt{5}$ | B. | 1+2$\sqrt{5}$或1+4$\sqrt{5}$ | C. | 9+2$\sqrt{5}$或9-2$\sqrt{5}$ | D. | 10+2$\sqrt{5}$或10-2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
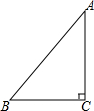 在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com