

分析 (1)利用作一个角等于已知角的方法,即可作出所求直线;
(2)易求得∠BAP=∠GPF,∠ABP=∠PGF=90°,又由AP=PF,即可证得△ABP≌△PGF,继而证得结论;
(3)首先证得FG=CG,即可得△FCG是等腰直角三角形,继而求得答案;
(4)首先作CH⊥PF于H,易证得△PHC∽△PGF,由相似三角形的对应边成比例,可得$\frac{BP}{BC}=\frac{3}{4}$,然后设BP=3a,则PC=a,PG=4a,FG=CG=3a,分别求得FC,HC,继而求得答案.
解答  (1)解:如图1所示:
(1)解:如图1所示:
(2)证明:∵PE⊥AP,
∴∠APE=90°.
∴∠APB+∠GPF=90°,
又∵∠APB+∠BAP=90°,
∴∠BAP=∠GPF,
又∵FG⊥BC,
∴∠ABP=∠PGF=90°,
在△ABP与△PGF中,
$\left\{\begin{array}{l}{∠ABP=∠PGF}\\{∠BAP=∠GPF}\\{AP=PF}\end{array}\right.$,
∴△ABP≌△PGF(AAS).
∴FG=BP;
(3)解:由(2)知AB=PG,
∵AB=BC,
∴BC=PG.
∴BC-PC=PG-PC.
∴BP=CG,
又∵FG=BP,
∴FG=CG.
又∵∠CGF=90°,
∴∠FCG=45°;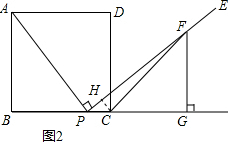 (4)解:如图2,作CH⊥PF于H,
(4)解:如图2,作CH⊥PF于H,
∵∠HPC=∠GPF,∠CHP=∠FGP=90°,
∴△PHC∽△PGF.
∴$\frac{HC}{GF}=\frac{PC}{PF}$,
根据$\frac{BP}{BC}=\frac{3}{4}$,
设BP=3a,则PC=a,PG=4a,FG=CG=3a,
∴PF=$\sqrt{P{G}^{2}+F{G}^{2}}$=5a,CF=$\sqrt{C{G}^{2}+F{G}^{2}}$=3$\sqrt{2}$a,
∴$\frac{HC}{3a}=\frac{a}{5a}$.
∴HC=$\frac{3}{5}$a,
∴sin∠CFP=$\frac{HC}{CF}=\frac{\frac{3}{5}a}{3\sqrt{2}a}$=$\frac{\sqrt{2}}{10}$.
点评 此题属于四边形的综合题,考查了矩形的性质、相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质以及勾股定理等知识.注意准确作出辅助线是解此题的关键.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 酷爱写诗的陈老师,某日到南山采风,结束后步行下山回家,发现下山路AB为一条坡度为i=5:12的斜坡,在斜坡下端B处有一座塔,陈老师在A处测得塔顶P的俯角为14°,沿斜坡前行65米到达B处,请根据以上条件求塔的高度BP.(参考数据:tan14°≈0.25,sin14°≈0.24,cos14°≈0.97)
酷爱写诗的陈老师,某日到南山采风,结束后步行下山回家,发现下山路AB为一条坡度为i=5:12的斜坡,在斜坡下端B处有一座塔,陈老师在A处测得塔顶P的俯角为14°,沿斜坡前行65米到达B处,请根据以上条件求塔的高度BP.(参考数据:tan14°≈0.25,sin14°≈0.24,cos14°≈0.97)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com