
【题目】如图,点D在△ABC边延长线上,点O是边AC上一个动点,过O作直线EF∥BC,交∠BCA的平分线于点F,交∠BCA的外角平分线于E.当点O在线段AC上移动(不与点A,C重合)时,下列结论不一定成立的是( )
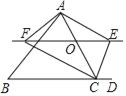
A. 2∠ACE=∠BAC+∠B B. EF=2OC C. ∠FCE=90° D. 四边形AFCE是矩形
【答案】D
【解析】
依据三角形外角性质,角平分线的定义,以及平行线的性质,即可得到2∠ACE=∠BAC+∠B,EF=2OC,∠FCE=90°,进而得到结论.
解:∵∠ACD是△ABC的外角,
∴∠ACD=∠BAC+∠B,
∵CE平分∠DCA,
∴∠ACD=2∠ACE,
∴2∠ACE=∠BAC+∠B,故A选项正确;
∵EF∥BC,CF平分∠BCA,
∴∠BCF=∠CFE,∠BCF=∠ACF,
∴∠ACF=∠EFC,
∴OF=OC,
同理可得OE=OC,
∴EF=2OC,故B选项正确;
∵CF平分∠BCA,CE平分∠ACD,
∴∠ECF=∠ACE+∠ACF=![]() ×180°=90°,故C选项正确;
×180°=90°,故C选项正确;
∵O不一定是AC的中点,
∴四边形AECF不一定是平行四边形,
∴四边形AFCE不一定是矩形,故D选项错误,
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间的铁路交通设有特快列车和普通快车两种车次,某天一辆普通快车从甲地出发匀速向乙地行驶,同时另一辆特快列车从乙地出发匀速向甲地行驶,两车离甲地的路程S(千米)与行驶时间t(时)之间的函数关系如图所示.
(1)甲地到乙地的路成为________千米,普通快车到达乙地所用时间为_______小时.
(2)求特快列车离甲地的路程s与t之间的函数关系式.
(3)在甲、乙两地之间有一座铁路桥,特快列车到铁路桥后又行驶0.5小时与普通快车相遇,求甲地与铁路桥之间的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,李老师让同学们试着用角尺平分 ![]() (如图所示),有两组.
(如图所示),有两组.
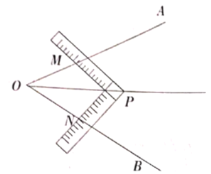
同学设计了如下方案:
方案①:将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度位于
之间,移动角尺使角尺两边相同的刻度位于![]() 上,且交点分别为
上,且交点分别为![]() ,即
,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.
的平分线.
方案②:在边![]() 上分别截取
上分别截取![]() ,将角尺的直角顶点
,将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度与点
之间,移动角尺使角尺两边相同的刻度与点![]() 重合,即
重合,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
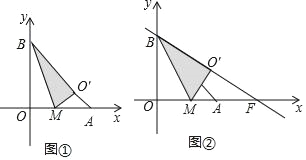
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=![]() 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
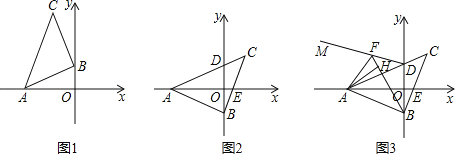
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),点C的坐标为 .
(2)如图2,若OA平分∠BAC,BC与x轴交于点E,若点C纵坐标为m,求AE的长.
(3)如图3,在(2)的条件下,点F在射线DM上,且∠ABF=∠ADF,AH⊥BF于点H,试探究BF、HFDF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开住乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间式(小时)之间的函数图象如图所示,则下列说法中错误的是( )
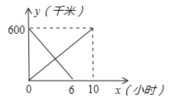
A. 客车比出租车晚4小时到达目的地B. 客车速度为60千米时,出租车速度为100千米/时
C. 两车出发后3.75小时相遇D. 两车相遇时客车距乙地还有225千米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com