
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABCM的面积.

【答案】(1)、6;(2)、9.
【解析】
试题分析:(1)、由四边形ABCD为平行四边形,得到对边平行且相等,且对角线互相平分,根据两直线平行内错角相等得到两对角相等,进而确定出三角形MND与三角形CNB相似,由相似得比例,得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;(2)、由相似三角形相似比为1:2,得到S△MND:S△CND=1:4,可得到△MND面积为1,△MCD面积为3,由S平行四边形ABCD=ADh,S△MCD=MDh=ADh,=4S△MCD,即可求得答案.
试题解析:(1)、∵平行四边形ABCD, ∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC, ∴△MND∽△CNB, ∴![]() ,
,
∵M为AD中点,所以BN=2DN, 设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x﹣1,
∴x+1=2(x﹣1), 解得:x=3, ∴BD=2x=6;
(2)、∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=1:2, ∴S△MND:S△CND=1:4, ∵△DCN的面积为2, ∴△MND面积为1,
∴△MCD面积为3, 设平行四边形AD边上的高为h, ∵S平行四边形ABCD=ADh,S△MCD=MDh=ADh,
∴S平行四边形ABCD=4S△MCD=12. ∴四边形ABCM的面积=9.


科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( ) 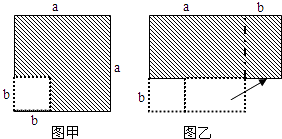
A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( ) 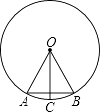
A.△OAB是等边三角形
B.弦AC的长等于圆内接正十二边形的边长
C.OC平分弦AB
D.∠BAC=30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师布置了两道解方程的作业题:
(1)选用合适的方法解方程:(x+1)(x+2)=6;
(2)用配方法解方程:2x2+4x-5=0.
以下是小明同学的作业:
(1)解:由(x+1)(x+2)=6, | (2)解:由2x2+4x-5=0, |
得x+1=2,x+2=3, | 得2x2+4x=5, |
所以x1=1,x2=1. | x2+2x= |
x2+2x+1= | |
(x+1)2= | |
x+1=± | |
x1=-1+ |
请你帮小明检查他的作业是否正确,把不正确的改正过来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A=40°,求∠DCB的度数;
(2)若AE=5,△DCB的周长为16,求△ABC的周长.
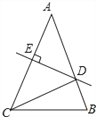
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高教师的综合素质,教育部门对全长沙市教师进行某项专业技能培训.为了解培训的效果,培训结束后随机抽取了部分参训老师进行技能测试,测试结果分成“不合格”、“合格”、“良好”、“优秀”四个等级,并绘制了如图所示的统计图,请根据统计图提供的信息,回答下列问题: 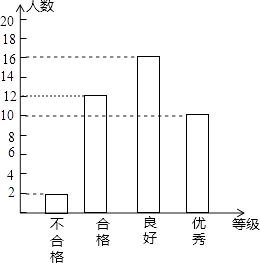
(1)培训结束后共抽取了名参训教师进行技能测试;
(2)从参加测试的人员中随机抽取一人进行技能展示,其测试结果为“优秀”的概率为;
(3)若全市有4000名参加培训的教师,请你估算获得“优秀”的总人数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 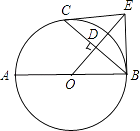
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于20.55与2.055这两个近似数,下列说法中,正确的是( ).
A.它们的有效数字与精确位数都不相同
B.它们的有效数字与精确位数都相同
C.它们的精确位数不相同,有效数字相同
D.它们的有效数字不相同,精确位数相同
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com