
分析 首先根据a,b互为倒数,可得ab=1;再根据c、d互为相反数,可得c+d=0;再根据|x|=3,可得x2=32=9;然后应用代入法,求出x2-(ab+c+d)+|ab+3|的值是多少即可.
解答 解:∵a,b互为倒数,
∴ab=1;
∵c、d互为相反数,
∴c+d=0;
∵|x|=3,
∴x2=32=9;
x2-(ab+c+d)+|ab+3|
=9-(1+0)+|1+3|
=9-1+4
=12
点评 此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
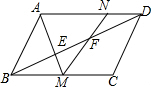 如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.
如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com