
【题目】如图,反比例函数![]() 的图象与直线y=kx+b相交于点A、B,点A的坐标为(2,4),直线AB交y轴于点C(0,2),交x轴于点E.
的图象与直线y=kx+b相交于点A、B,点A的坐标为(2,4),直线AB交y轴于点C(0,2),交x轴于点E.
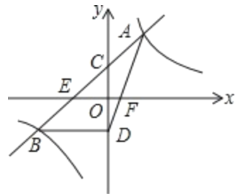
(1)求反比例函数与一次函数的表达式;
(2)求点E、B的坐标;
(3)过点B作BD⊥y轴,垂足为D,连接AD交x轴于点F,求![]() 的值.
的值.
【答案】(1)反比例函数表达式为![]() ,一次函数表达式为
,一次函数表达式为![]() ;(2)E (-2,0) ,B(-4,-2);(3)
;(2)E (-2,0) ,B(-4,-2);(3)![]()
【解析】
(1)采用待定系数法求反比例函数和一次函数表达式;
(2)求直线AC与x轴的交点,与反比例函数的交点即可得到E、B的坐标;
(3)由EF∥BD得到△AEF∽△ABD,利用坐标系中两点间的距离公式求出AE,AB得到相似比,利用面积比等于相似比的平方即可得到答案.
解:(1)∵反比例函数![]() 经过A (2,4),
经过A (2,4),
∴![]() ,解得
,解得![]() .
.
∴反比例函数表达式为![]()
∵直线y=kx+b经过A (2,4),C(0,2)
∴![]() ,解得
,解得![]() ,
,
∴一次函数表达式为![]()
(2)∵直线![]() 与x轴交于E点,当y=0时,
与x轴交于E点,当y=0时,![]() ,即
,即![]() ,
,
∴E点坐标为(-2,0)
将一次函数![]() 与反比例函数
与反比例函数![]() 联立得,
联立得,
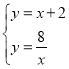 ,解得
,解得![]() 或
或![]()
∵A点坐标为(2,4)
∴B点坐标为(-4,-2)
(3)∵点A的坐标为(2,4),E点坐标为(-2,0),B点坐标为(-4,-2)
∴![]()
![]()
∴![]()
∵EF⊥y轴,BD⊥y轴
∴EF∥BD
∴△AEF∽△ABD
∴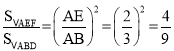


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
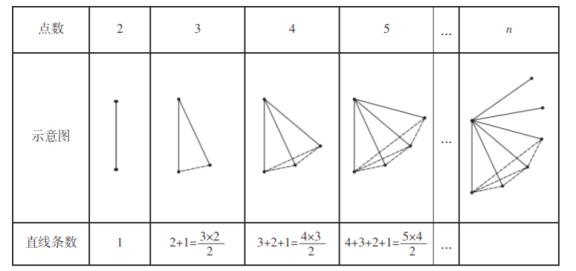
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
(1)请用无刻度的直尺和圆规,过点B作直线m⊥l,交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)
(2)求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
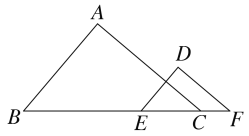
【题目】如图,已知点B、E、C、F在同一条直线上,∠A= ∠D,要使△ABC∽△DEF,还需添加一个条件,则添加的条件可以是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
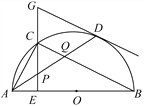
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD,G是BC边上ー点,连接AG,分别以AG和BG为直角边作等腰Rt△AGF和等腰Rt△GBE,使∠GBE=∠AGF=90°,点E,F在BC下方,连接EF.
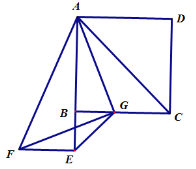
求证:①∠BAG=∠BGF,
②CG=EF:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com