
【题目】如图①,矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止. 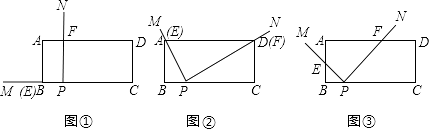
(1)特殊情形:如图②,发现当PM过点A时,PN也恰巧过点D,此时,△ABP△PCD(填“≌”或“~”);
(2)类比探究:如图③,在旋转过程中, ![]() 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由.
【答案】
(1)~
(2)解:在旋转过程中, ![]() 的值为定值.
的值为定值.
证明:如图③所示,过点F作FG⊥BC于G,则∠B=∠FGP,
∵∠MPN=90°,∠B=90°,
∴∠BEP+∠EPB=90°=∠CPF+∠EPB,
∴∠BEP=∠CPF,
∴△EBP∽△GPF,
∴ ![]() =
= ![]() ,
,
∵矩形ABGF中,FG=AB=2,而PB=1,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
即 ![]() 的值为定值
的值为定值 ![]() .
.
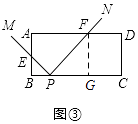
【解析】解:(1)如图②所示, 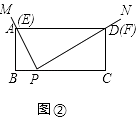
∵∠MPN=90°,∠B=90°,
∴∠BAP+∠APB=90°=∠CPD+∠APB,
∴∠BAP=∠CPD,
又∵∠B=∠C,
∴△ABP∽△PCD;
所以答案是:∽;
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握相似三角形的判定(相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS))的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α= ![]() ,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或
,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或 ![]() ;④0<BE≤5,其中正确的结论是(填入正确结论的序号)
;④0<BE≤5,其中正确的结论是(填入正确结论的序号) 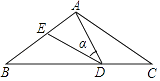
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E. 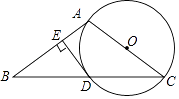
(1)求证:DE是⊙O的切线;
(2)若AC=10,BC=16,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴方程为x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,则正确的结论是( ) 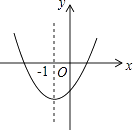
A.①②③④
B.②④⑤
C.①④⑤
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整. 原题:如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证: ![]() .
.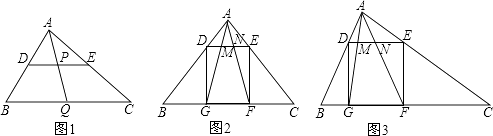
(1)尝试探究:在图1中,由DP∥BQ得△ADP△ABQ(填“≌”或“∽”),则 ![]() = , 同理可得
= , 同理可得 ![]() =
= ![]() ,从而
,从而 ![]() .
.
(2)类比延伸:如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交DE于M、N两点,若AB=AC=1,则MN的长为 .
(3)拓展迁移:如图3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交于DE于M、N两点,AB<AC,求证:MN2=DMEN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是⊙O外一点,PA和PB分别切⊙O于A、B两点,已知⊙O的半径为6cm,∠PAB=60°,若用图中阴影部分以扇形围成一个圆锥的侧面,则这个圆锥的高为 . 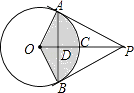
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 . 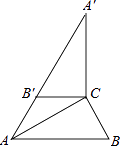
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com