
【题目】菱形ABCD中,∠B=60°,∠MAN=60°,射线AM交直线BC于点E,射线AN交直线CD于点F,连结EF,请解答下列问题:
(1)如图1,求证:EC+FC=AC;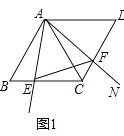
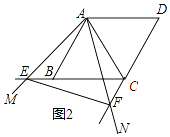
(2)将∠MAN绕点A旋转,如图2,如图3,请直接写出线段EC,FC,AC之间的数量关系,不需要证明;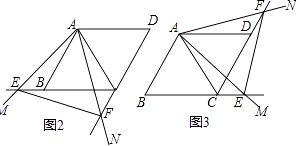
(3)若S菱形ABCD=18 ![]() ,∠CAE=30°,则CF=
,∠CAE=30°,则CF=
【答案】
(1)
解:如图1所示:
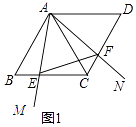
∵四边形ABCD为菱形,∠B=60°
∴AB=BC,∠ACF=∠B=60°.
又∵∠B=60°,
∴△ABC为等边三角形.
∴AC=BC=AB,∠BAC=60°.
又∵∠MAN=60°,
∴∠BAE=∠CAF.
在△ABE和△ACF中 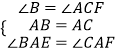 ,
,
∴△ABE≌△ACF(ASA).
∴BE=CF.
∴EC+CF=EC+BE=BC.
又∵BC=AC,
∴EC+CF=AC
(2)
解:如图2所示:AC+CF=EC.
∵四边形ABCD为菱形,∠B=60°
∴AB=BC,∠ACD=∠B=60°.
∴∠ACF=120°.
∵∠B=60°,AB=BC,
∴△ABC为等边三角形.
∴AC=BC=AB,∠ABC=60°.
∴∠ABE=120°.
∴∠ABE=∠ACF.
∵∠MAN=∠BAC=60°
∴∠BAE=∠CAF.
在△ABE和△ACF中 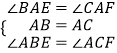 ,
,
∴△ABE≌△ACF(ASA).
∴BE=CF.
∴FC+BC=BE+BC=CE.
∵BC=AC,
∴FC+AC=CE.
如图3所示:
又∵BC=AC,
∴EC+CF=AC.
如图3所示:CF=AC+CE.
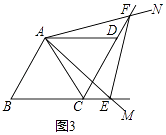
在△ACE和△ADF中 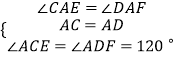 ,
,
△ACE≌△ADF(ASA).
∴CE=DF.
∴CF=CD+DF=CD+CE=AC+CE,即CF=AC+CE
(3)3或12
【解析】解:(3)如图1所示:
∵∠CAE=30°,∠CAB=60°,
∴AE平分∠CAB.
又∵AB=AC,
∴AE⊥BC,BE=CE.
∴AE= ![]() AB.
AB.
∵S菱形ABCD=18 ![]() ,
,
∴AB ![]() AB=18
AB=18 ![]() .
.
∴AB=6.
∴BE=EC=3.
∴CF=3.
如图3所示:
∵∠CAE=30°,∠BAC=60°,
∴∠BAE=90°.
又∵AB=6,∠B=60°,
∴BE=12.
∴CF=AC+CE=BC+CE=12.
综上所述,CF=3或CF=12.
所以答案是:3或12.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点P0的坐标为(![]() ,
,![]() ),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )
),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )

A. (![]() ,
,![]() ) B. (0,22018) C. (
) B. (0,22018) C. (![]() ,
,![]() ) D. (22018,0)
) D. (22018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
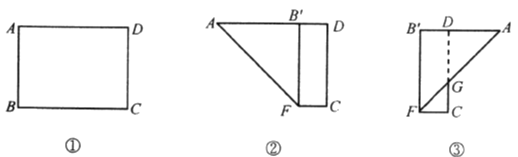
【题目】如图①,在长方形![]() 中,
中,![]() cm,
cm,![]() cm.现将其按下列步骤折叠:(1)将边
cm.现将其按下列步骤折叠:(1)将边![]() 向边
向边![]() 折叠,使边
折叠,使边![]() 落在边
落在边![]() 上,得到折痕
上,得到折痕![]() ,如图②;(2)将
,如图②;(2)将![]() 沿
沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,如图③.则所得梯形
,如图③.则所得梯形![]() 的周长等于( )
的周长等于( )
A. ![]() cm B.
cm B. ![]() cm
cm
C. ![]() cm D.
cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,则水的最大深度CD为( ) 
A.4cm
B.3cm
C.2cm
D.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为 , 则图中阴影部分的面积是 . 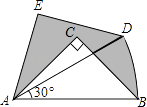
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.

(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com