
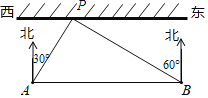
【题目】为了保证端午节龙舟赛在我市侨港海域顺利举办,某部门工作人员乘快艇到侨港海域考察水情,以每秒11米的速度沿平行于岸边的赛道AB由西向东行驶,在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
科目:初中数学 来源: 题型:
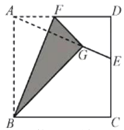
【题目】如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE,折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
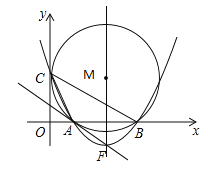
【题目】如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.
(1)则点A、B、C的坐标分别是A(__,__),B(__,__),C(__,__);
(2)设经过A、B两点的抛物线解析式为![]() ,它的顶点为F,求证:直线FA与⊙M相切;
,它的顶点为F,求证:直线FA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
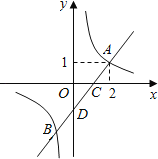
(1)求一次函数和反比例函数的解析式;
(2)求点C的坐标;
(3)结合图象直接写出不等式0<x+m≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
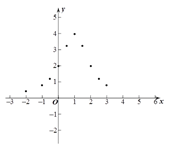
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点A(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣2,y1),(![]() ,y2)是抛物线上两点,则y1>y2,其中说法正确的是( )
,y2)是抛物线上两点,则y1>y2,其中说法正确的是( )
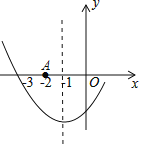
A.①②B.②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
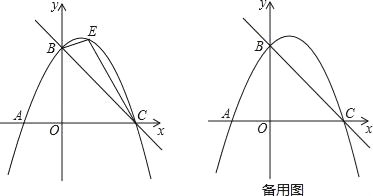
【题目】如图,直线y=﹣![]() x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
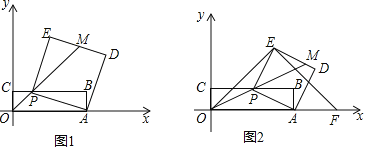
【题目】已知:如图1,矩形OABC的两个顶点A,C分别在x轴,y轴上,点B的坐标是(8,2),点P是边BC上的一个动点,连接AP,以AP为一边朝点B方向作正方形PADE,连接OP并延长与DE交于点M,设CP=a(a>0).
(1)请用含a的代数式表示点P,E的坐标.
(2)连接OE,并把OE绕点E逆时针方向旋转90°得EF.如图2,若点F恰好落在x轴的正半轴上,求a与![]() 的值.
的值.
(3)①如图1,当点M为DE的中点时,求a的值.
②在①的前提下,并且当a>4时,OP的延长线上存在点Q,使得EQ+![]() PQ有最小值,请直接写出EQ+
PQ有最小值,请直接写出EQ+![]() PQ的最小值.
PQ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com