
分析 (1)根据判别式的意义得到△=(4k+2)2-8(2k2+1)=16k-4>0,然后解不等式解即可;
(2)根据判别式的意义得到△=(4k+2)2-8(2k2+1)=16k-4=0,求出k的值即可;
(3)根据判别式的意义得到△=(4k+2)2-8(2k2+1)=16k-4<0,然后解不等式解即可.
解答 解:△=(4k+2)2-8(2k2+1)=16k-4;
(1)当k>$\frac{1}{4}$时,方程有两个不相等的实数根.
(2)当k=$\frac{1}{4}$时,方程有两个相等的实数根.
(3)当k<$\frac{1}{4}$时,方程没有实数根.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.


科目:初中数学 来源: 题型:解答题
 已知如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点D从点A出发,以每秒1cm的速度沿射线AC运动,如果在运动过程中△ABD为等腰三角形,求出点D运动的时间t.
已知如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点D从点A出发,以每秒1cm的速度沿射线AC运动,如果在运动过程中△ABD为等腰三角形,求出点D运动的时间t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
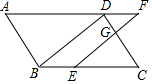 如图,在平行四边形ABCD中,点E在边BC上,过点E作BD的平行线交DC于点G、交AD的延长线于点F.
如图,在平行四边形ABCD中,点E在边BC上,过点E作BD的平行线交DC于点G、交AD的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请将数轴补全,然后把数-4,1,0,-|-1$\frac{1}{2}}$|,-(-5)表示在数轴上,并按从小到大的顺序,从左到右串个糖葫芦,把数填在“○”内.
请将数轴补全,然后把数-4,1,0,-|-1$\frac{1}{2}}$|,-(-5)表示在数轴上,并按从小到大的顺序,从左到右串个糖葫芦,把数填在“○”内.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com