
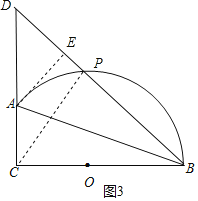
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=![]() ,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
(1)求半径OB的长;
(2)如果点P是弧AB的中点,联结PC,求∠PCB的正切值;
(3)如果BA平分∠PBC,延长BP、CA交于点D,求线段DP的长.
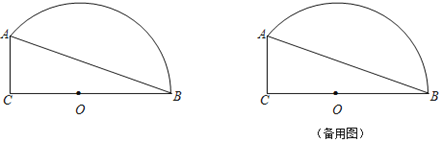
【答案】(1)OB=9;(2)∠PCB的正切值=![]() (3)PD=
(3)PD=![]() .
.
【解析】
(1)根据勾股定理得到AB=![]() =12
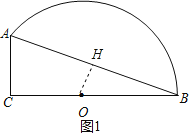
=12![]() ,如图1,过O作OH⊥AB于H,根据相似三角形的性质即可得到结论;
,如图1,过O作OH⊥AB于H,根据相似三角形的性质即可得到结论;
(2)如图2,连接OP交AB于H,根据垂径定理得到OP⊥AB,AH=BH=![]() AB=6
AB=6![]() ,根据勾股定理得到OH=3,过P作PM⊥OB于M,证明△OBH≌△OPM ,得到
,根据勾股定理得到OH=3,过P作PM⊥OB于M,证明△OBH≌△OPM ,得到![]()
![]()
![]()
![]() 根据三角函数的定义即可得到结论;
根据三角函数的定义即可得到结论;
(3)如图3,过A作AE⊥BD于E,连接CP,根据角平分线的性质得到AE=AC=4![]() ,根据相似三角形的性质得到AD=
,根据相似三角形的性质得到AD=![]() ,根据全等三角形的性质得到BE=BC=16,根据勾股定理和三角形的面积公式即可得到结论.
,根据全等三角形的性质得到BE=BC=16,根据勾股定理和三角形的面积公式即可得到结论.
解:(1)∵Rt△ABC中,∠ACB=90°,AC=![]() ,BC=16,
,BC=16,
∴AB=![]() =12
=12![]() ,
,
如图1,过O作OH⊥AB于H,
则BH=![]() AB=6
AB=6![]() ,
,
∵∠BHO=∠ACB=90°,∠B=∠B,
∴△BHO∽△BCA,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴OB=9;
(2)如图2,连接OP交AB于H,
∵点P是弧AB的中点,
∴OP⊥AB,AH=BH=![]() AB=6
AB=6![]() ,
,
在Rt△BHO中,OH=![]() =
=![]() =3,
=3,
过P作PM⊥OB于M,

在△OBH与△OPM中,
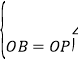
∴△OBH≌△△OPM (AAS),
![]()
![]()
![]()
![]()
∴∠PCB的正切值![]()
(3)如图3,过A作AE⊥BD于E,连接CP,
∵BA平分∠PBC,AC⊥BC,
∴AE=AC=4![]() ,
,
∵∠AED=∠ACB=90°,∠D=∠D,
∴△ADE∽△BDC,
∴![]() =
=![]() ,
,
设DE=x,
∴![]() =
=![]() ,
,
∴AD=![]() ,
,
在Rt△ACB与Rt△AEB中,![]() ,
,
∴Rt△ACB≌Rt△AEB(HL),
∴BE=BC=16,
∵CD2+BC2=BD2,
∴(4![]() +
+![]() )2+162=(16+x)2,
)2+162=(16+x)2,
解得:x=![]() ,
,
∴AD=![]() ,BD=16+
,BD=16+![]() =
=![]() ,
,
∴CD=![]() ,
,
∵BC是⊙的直径,
∴CP⊥BD,
∴CP=![]() =
=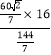 =
=![]() ,
,
∴PD=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
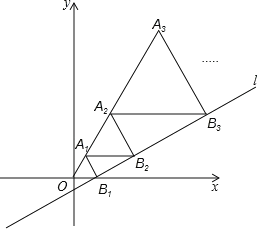
【题目】在直角坐标系中,直线l1:y![]() 与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1,作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3,为边长作等边△A3A2B3…,则等边△A2019A2018B2019的边长是______.
与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1,作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3,为边长作等边△A3A2B3…,则等边△A2019A2018B2019的边长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是⊙O的直径,过⊙O上一点C作直线l,AD⊥l于点D.
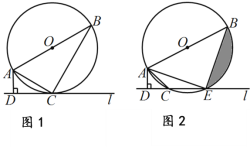
(1)连接AC、BC,若∠DAC=∠BAC,求证:直线l是⊙O的切线;
(2)将图1的直线l向上平移,使得直线l与⊙O交于C、E两点,连接AC、AE、BE, 得到图2. 若∠DAC=45°,AD=2cm,CE=4cm,求图2中阴影部分(弓形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为半圆上一点,AC<BC.
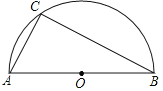
(1)请用直尺(不含刻度)与圆规在BC上作一点D,使得直线OD平分ABC的周长;(不要求写作法,但要保留作图痕迹)
(2)在(1)的条件下,若AB=10,OD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
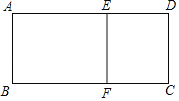
【题目】如图所示,用一根长度为18米的原材料制作一个矩形窗户边框(即矩形ABFE和矩形DCFE),原材料刚好全部用完,设窗户边框AB长度为x米,窗户总面积为S平方米(注:窗户边框粗细忽略不计).
(1)求S与x之间的函数关系式;
(2)若窗户边框AB的长度不少于2米,且边框AB的长度小于BC的长度,求此时窗户总面积S的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
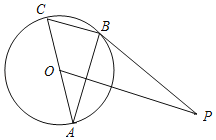
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=4,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
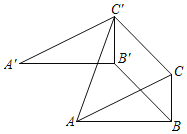
【题目】定义:有一组邻边相等的凸四边形叫做等邻边四边形.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB'的方向平移,得到A'B'C',连接AC',CC',若四边形ABCC'是等邻边四边形,则平移距离BB'的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小魏探究学习函数的经验,对函数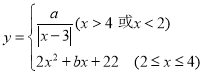 的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
(1)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出:![]() _______,
_______,![]() ______,
______,![]() _______.
_______.
(2)画出该函数图像.
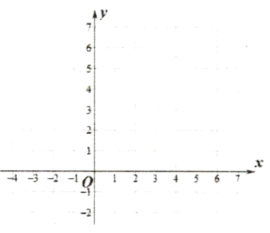
(3)写出该函数的一条性质:_______________.
(4)一次函数![]() 与该函数图像至少有三个交点,则
与该函数图像至少有三个交点,则![]() 的范围_______.
的范围_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com