
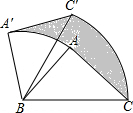
 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
分析 过点C′作C′E⊥BC于点E,证明C′、A、E在一条直线上,求出∠A′BA=∠C′BC=60°,BC=3$\sqrt{2}$,再根据S阴影=S扇形C′BC+S△C′A′B-S扇形A′BA-S△ABC,即可解答.
解答 解:如图,过点C′作C′E⊥BC于点E,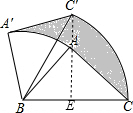
∵点C′恰好落在边BC上的高所在的直线上,AB=AC,
∴C′、A、E在一条直线上,
∴BE═EC=$\frac{1}{2}$BC,
∵BC=BC′,
∴BE=$\frac{1}{2}$BC′,
∵∠BEC′=90°,
∴∠BC′E=30°,
∴∠C′BE=60°,
∵AB=AC=3,∠A=90°,
∴∠ABC=∠ACB=45°,BC=$\sqrt{{3}^{2}+{3}^{2}}=\sqrt{18}=3\sqrt{2}$,
∵△C′A′B≌△CAB,
∴∠A′BC′=∠ABC=45°,
∴∠A′BA=∠C′BC=60°,
∴S阴影=S扇形C′BC+S△C′A′B-S扇形A′BA-S△ABC=$\frac{60π•(3\sqrt{2})^{2}}{360}+\frac{1}{2}×3×3-\frac{60π•{3}^{2}}{360}-\frac{1}{2}×3×3$=$\frac{3}{2}π$.
故选:B.
点评 本题考查了扇形的面积计算及旋转的性质,利用旋转的性质得出Rt△AB'B'≌Rt△ACB是解答本题的关键,注意掌握不规则图形的面积计算.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )
如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )| A. | p | B. | q | C. | m | D. | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
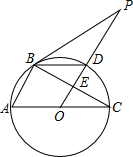 如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com