【题目】如图，在测量“河流宽度”的综合与实践活动中，小李同学设计的方案及测量数据如下：在河对岸边选定一个目标点A，在近岸取点B，C，D (点B，C，D在同一条直线上)，AB⊥BD，∠ACB＝45°，CD＝20米，且．若测得∠ADB＝25°，请你帮助小李求河的宽度AB.（sin25°≈0.42，cos25°≈0.91，tan25°≈0.47，结果精确到0.1米）．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】已知△ABC∽△A′B′C′，AB＝4 cm，A′B′＝3 cm，AD，A′D′分别为△ABC与△A′B′C′的中线，下列结论中：①AD∶A′D′＝4∶3；②△ABD∽△A′B′D′；③△ABD∽△A′B′C′；④△ABC与△A′B′C′对应边上的高之比为4∶3.其中结论正确的序号是_____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝ax2﹣2ax﹣3（a≠0）的图象经过点A．
（1）求二次函数的对称轴；
（2）当A（﹣1，0）时，
①求此时二次函数的表达式；
②把y＝ax2﹣2ax﹣3化为y＝a（x﹣h）2+k的形式，并写出顶点坐标；
③画出函数的图象．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
，
与
的部分对应值如下表所示：
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断：
①抛物线的顶点为
；
②
；
③关于的方程
的解为
；
④
．
其中，正确的有___________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在矩形ABCD中，P为CD边上一点（DP＜CP），∠APB＝90°．M在AB上，且∠APM＝∠APD，过点B作BN∥MP交DC于点N．
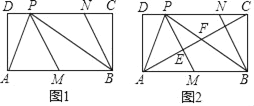
（1）求证：四边形PMBN是菱形；
（2）求证：ADBC＝DPPC；
（3）如图2，连接AC，分别交PM，PB于点E，F，若DP＝1，AD＝2，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于平面内任意一个角的“夹线圆”，给出如下定义：如果一个圆与这个角的两边都相切，则称这个圆为这个角的“夹线圆”.例如：在平面直角坐标系xOy中，以点（1，1）为圆心，1为半径的圆是x轴与y轴所构成的直角的“夹线圆”.
(1)下列各点中，可以作为x轴与y轴所构成的直角的“夹线圆”的圆心的点是哪些；
A（2，2），B（3，1），C（-1，0），D（1，-1）
(2)若⊙P为y轴和直线 l：
所构成的锐角的“夹线圆”，且⊙P的半径为1，求点P的坐标.
(3)若 ⊙Q为x轴和直线
所构成的锐角的“夹线圆”，且⊙Q的半径
，直接写出点Q横坐标
的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点C是⊙O上一点，连接BC，AC，OD⊥BC于E．
（1）求证：OD∥AC；
（2）若BC＝8，DE＝3，求⊙O的直径．
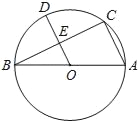
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学运动队有短跑、长跑、跳远、实心球四个训练小队，现将四个训练小队队员情况绘制成如下不完整的统计图:
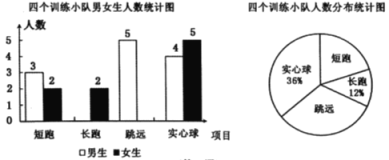
(l)学校运动队的队员总人数为 人，扇形统计图中短跑训练小队所对应圆心角的度数为 ;
(2)补全条形统计图，并标明数据;
(3)若在短跑训练小组中随机选取2名同学进行比赛，请用列举法(画树状图或列表)求所选取的这两名同学恰好是一男一女的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线l：y=ax2+bx+c（a，b，c均不为0）的顶点为M，与y轴的交点为N，我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．
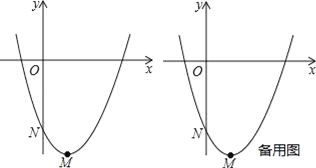
（1）如图，抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ，衍生直线的解析式是 ；
（2）若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1，求这条抛物线的解析式；
（3）如图，设（1）中的抛物线y=x2﹣2x﹣3的顶点为M，与y轴交点为N，将它的衍生直线MN先绕点N旋转到与x轴平行，再沿y轴向上平移1个单位得直线n，P是直线n上的动点，是否存在点P，使△POM为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
