练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．某中学要了解初二学生的视力情况，在全校初二年级中抽取25名学生进行检测，在这个问题中，样本是抽取25名学生的视力情况．

    分析 总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．

    解答 解：某中学要了解初二学生的视力情况，在全校初二年级中抽取25名学生进行检测，在这个问题中，样本是抽取25名学生的视力情况，
    故答案为：抽取25名学生的视力情况．

    点评 此题考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．在△ABC中，点D、E分别在AB、AC边上，∠B=∠AED，那么下列结论中不正确的是（　　）
    A．AD：AC=AE：ABB．AD•AB=AE•ACC．DE：BC=AD：ACD．DE：BC=AD：AB

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知“x与y的和不大于6”；用不等式表示为：x+y≤6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．先化简，再求值：（2a-1）2-（1-2a）（2a+1），其中a=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

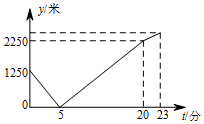    20．早晨，小刚沿着通往学校唯一的一条路（直路）上学，途中发现忘带饭盒，停下往家里打电话，妈妈接到电话后带上饭盒马上赶往学校，同时小刚返回，两人相遇后，小刚立即赶往学校，妈妈回家，15分钟妈妈到家，再经过3分钟小刚到达学校，小刚始终以100米/分的速度步行，小刚和妈妈的距离y（单位：米）与小刚打完电话后的步行时间t（单位：分）之间的图象如图所示，根据题意填空：
    ①打电话时，小刚和妈妈的距离为1250米；
    ②打完电话后，经过23分钟小刚到达学校；
    ③小刚和妈妈相遇后，妈妈回家的速度为50米/分；
    ④小刚家与学校的距离为2550米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．若$\frac{a-b}{b}$=$\frac{3}{4}$，则$\frac{b}{a}$=$\frac{4}{7}$；若$\frac{x}{4}$=$\frac{y}{3}$=$\frac{z}{2}$，则$\frac{x-y+3z}{x}$=$\frac{7}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．在代数式$\frac{1}{2}$x2-3x，$\frac{2{x}^{2}y}{π}$，$\frac{1}{x}$，-6，a，0中，单项式有4个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知关于x的分式方程$\frac{m}{x-1}+\frac{3x}{1-x}=2$的有增根，则m的值是3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在平面直角坐标系中，点P（m，m）（m＞0）是过原点的直线上的动点．以P为端点在OP两侧作射线，其中射线PA交x轴于点B，交y轴于点A（0，m-a），射线PC交x轴于点C （m+a，0），m＞a＞0．是否存在点P，使得以P，B，C为顶点的三角形与△OAC相似？若存在，求此时tan∠OPC的值；若不存在．请说明理由．

    查看答案和解析>>

    同步练习册答案