
【题目】如图1,两个形状、大小完全相同的含有30°,60°的三角板按如图所示放置,PA、PB与直线MN重合,且三角板PAC和三角板PBD均可以绕点P逆时针旋转。

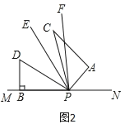
(1)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF的度数。
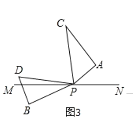
(2)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3°/s,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/s。在两块三角板旋转过程中(PC转到PM重合时,两三角板都停止转动),设两块三角板旋转的时间为ts,则∠BPN= °,∠CPD= °(用含t的式子表示,并化简);以下两个结论:①![]() 为定值;②∠BPN+∠CPD为定值,正确的是 (填序号)。
为定值;②∠BPN+∠CPD为定值,正确的是 (填序号)。

【答案】(1)∠EPF=30゜;(2)(180-2t),(90-t);①.
【解析】
(1)设∠CPE=∠DPE=x,∠CPF=y,则∠APF=∠DPF=2x+y,进而利用∠CPA=60゜求出即可;
(2)设运动时间为t秒,则∠BPM=2t,即可表示出∠CPD和∠BPN的度数,然后再代入①②中计算即可得出答案.
解:(1)如图2,设∠CPE=∠DPE=x,∠CPF=y,
则∠APF=∠DPF=2x+y,
∵∠CPA=60゜,
∴y+2x+y=60゜,
∴x+y=30゜,
∴∠EPF=x+y=30゜.
(2)由题意得∠BPM=2t,
∴∠BPN=180-2t,∠DPM=30-2t,∠APN=3t.
∴∠CPD=180-∠DPM-∠CPA-∠APN=90-t,
∴![]() ,所以①正确.
,所以①正确.
因为∠BPN+∠CPD=180-2t+90-t=270-3t,可以看出∠BPN+∠CPD随着时间t的变化而变化,不为定值,所以结论②错误.
故答案为:(180-2t),(90-t);①.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.

(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中有4个点:A(0,2),B(﹣2,﹣2),C(﹣2,2),D(3,3).
(1)在正方形网格中画出△ABC的外接圆⊙M,圆心M的坐标是 ;
(2)若EF是⊙M的一条长为4的弦,点G为弦EF的中点,求DG的最大值;
(3)点P在直线MB上,若⊙M上存在一点Q,使得P、Q两点间距离小于1,直接写出点P横坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.
(1) 采用树形图法(或列表法)列出两次摸球出现的所有可能结果;
(2) 求摸出的两个球号码之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每一个小正方形的边长为1.△ABC的三个顶点都在格点上,A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC向右平移6个单位的△A1B1C1,并写出C1的坐标 ;
(3)请画出△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.

(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com