
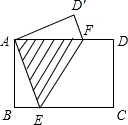
 如图,长方形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分△AEF的面积.
如图,长方形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分△AEF的面积. 分析 要求重叠部分△AEF的面积,选择AF作为底,高就等于AB的长;而由折叠可知∠AEF=∠CEF,由平行得∠CEF=∠AFE,代换后,可知AE=AF,问题转化为在Rt△ABE中求AE.
解答 解:设AE=x,由折叠可知,EC=x,BE=4-x,
在Rt△ABE中,AB2+BE2=AE2,即32+(4-x)2=x2,
解得:x=$\frac{25}{8}$,
由折叠可知∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF=$\frac{25}{8}$,
∴S△AEF=$\frac{1}{2}$×AF×AB=$\frac{1}{2}$×$\frac{25}{8}$×3=$\frac{75}{16}$.
点评 本题考查的是图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应角相等.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{2(x+\frac{y}{2})=99}\\{\frac{x}{2}+y=66}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=66}\\{\frac{x}{2}+y=99}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{2}+y=66}\\{\frac{x}{2}+2y=99}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=99}\\{2x+y=66}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).
如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com