运用平方差,完全平方公式解方程:
(1)16(x-1)2=225
(2)4x2-4x+1=x2-6x+9
(3)9(x+1)2=4(x-1)2
(4)x2-4x+4=(3-2x)2
【答案】
分析:平方差公式为:a
2-b
2=(a-b)(a+b),完全平方公式为:a
2±2ab+b
2=(a±b)
2.
解答:解:(1)16(x-1)
2-15
2=0,
所以[4(x-1)+15][4(x-1)-15]=0,
即4x+11=0,4x-19=0,
得x
1=-
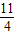
,x
2=
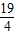
.
(2)方程变为(2x-1)
2-(x-3)
2=0,
所以[(2x-1)+(x-3)][(2x-1)-(x-3)]=0,
即3x-4=0,x+2=0,
得x
1=

,x
2=-2.
(3)原方程变为[3(x+1)]
2-[2(x-1)]
2=0,
所以[3(x+1)+2(x-1)][3(x+1)-2(x-1)]=0,
即(5x+1)(x+5)=0,
得x
1=-

,x
2=-5.
(4)(x-2)
2=(3-2x)
2.
(x-2)
2-(3-2x)
2=0,
(x-2+3-2x)(x-2-3+2x)=0,
(1-x)(3x-5)=0,
所以x
1=1,x
2=

.
点评:运用因式分解法解一元二次方程,能提公因式动用提公因式法,能运用完全平方式或平方差就用其公式来降次求解.

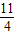 ,x2=
,x2=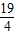 .
. ,x2=-2.
,x2=-2. ,x2=-5.
,x2=-5. .
.
