
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
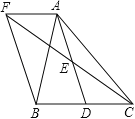
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
【答案】解:(1)BD=CD。理由如下:
∵AF∥BC,∴∠AFE=∠DCE。
∵E是AD的中点,∴AE=DE。
∵在△AEF和△DEC中,∠AFE=∠DCE,∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEC(AAS)。∴AF=CD。
∵AF=BD,∴BD=CD。
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形。理由如下:
∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形。
∵AB=AC,BD=CD,∴∠ADB=90°。
∴![]() AFBD是矩形。
AFBD是矩形。
【解析】
试题(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等,根据全等三角形对应边相等可得AF=CD,再利用等量代换即可得证;
(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90°,由等腰三角形三线合一的性质可知必须是AB=AC.
试题解析:(1)BD=CD.
理由如下:依题意得AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,
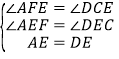 ,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,
∴AFBD是矩形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】有一组数,按照下列规律排列:
1,
2,3,
6,5,4,
7,8,9,10,
15,14,13,12,11,
16,17,18,19,20,21,
……
数字5在第三行左数第二个,我们用(3,2)点示5的位置,那点这组成数里的数字100的位置可以表示为( )
A. (14,9) B. (14,10) C. (14,11) D. (14,12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.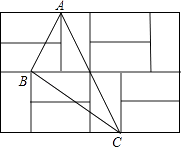
(1)求每个小矩形的长与宽;
(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
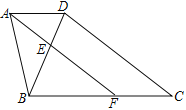
【题目】如图,在四边形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线分别交BD、BC于点E、F,且AE∥CD
(1) 求AD的长;
(2) 若∠C=30°,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. 
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y= ![]() (x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( ) 
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,点D是弧BC的中点,DE⊥AC于点E,DE⊥AB于点F. 
(1)求证:DE是⊙O的切线;
(2)若OF=2,求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
我们知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为n+n+n+…+n,即n2.这样,该三角形数阵中共有![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2.
个圆圈,所有圆圈中数的和为12+22+32+…+n2.
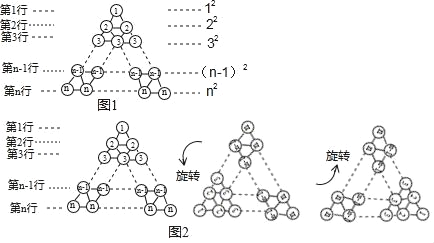
(规律探究)
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
(解决问题)
根据以上发现,计算:![]() 的结果为 .
的结果为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com