Question

已知直角坐标系中有一点A（-4，3），点B在x轴上，△AOB是等腰三角形．
（1）求满足条件的所有点B的坐标；
（2）求过O，A，B三点且开口向下的抛物线的函数表达式（只需求出满足条件的一条即可）；
（3）在（2）中求出的抛物线上存在点P，使得以O，A，B，P四点为顶点的四边形是梯形，求满足条件的所有点P的坐标及相应梯形的面积．

Answer 1

分析：（1）根据点A的坐标，易求得OA=5，若△AOB是等腰三角形，应分三种情况考虑：
①OA=OB=5，由于点B的位置不确定，因此要分B在x轴正、负半轴两种情况求解，已知了OB的长，即可得到点B的坐标；
②OA=AB=5，此时点B只能在x轴负半轴上，那么点B的横坐标应为点A横坐标的2倍，可据此求得点B的坐标；
③AB=OB=5，此时点B只能在x轴负半轴上，可在x轴上截取AD=OA，通过构建相似三角形：△OBA∽△OAD，通过所得比例线段来求出OB的长，从而得到点B的坐标．
（2）任选一个（1）题所得的B点坐标，利用待定系数法求解即可．
（3）解此题时，虽然不同的抛物线有不同的解，但解法一致；分两种情况：
①OA∥BP时，可分别过A、P作x轴的垂线，设垂足为C、E，易证得△AOC∽△PBE，根据所得比例线段，即可求得点P的坐标．而梯形ABPO的面积可化为△ABO、△PBO的面积和来求出．
②OP∥AB时，方法同上，过P作PF⊥x轴于F，然后通过相似三角形：△ABC∽△POF，来求出P点坐标，梯形面积求法同上．（当OA=AB时，两种情况的点P正好关于抛物线对称轴对称，可据此直接求出P点坐标，避免重复计算．）

解答：解：作AC⊥x轴，由已知得OC=4，AC=3，OA=

OC2+AC2

=5．
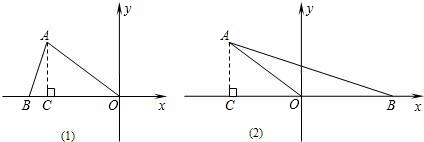
（1）当OA=OB=5时，
如果点B在x轴的负半轴上，如图（1），点B的坐标为（-5，0）；
如果点B在x轴的正半轴上，如图（2），点B的坐标为（5，0）；

当OA=AB时，点B在x轴的负半轴上，如图（3），BC=OC，则OB=8，点B的坐标为（-8，0）；
当AB=OB时，点B在x轴的负半轴上，如图（4），在x轴上取点D，使AD=OA，可知OD=8．
由∠AOB=∠OAB=∠ODA，可知△AOB∽△ODA，
则

OB

OA

=

OA

OD

，
解得OB=

25

8

，
点B的坐标为（-

25

8

，0）．


（2）当AB=OA时，抛物线过O（0，0），A（-4，3），B（-8，0）三点，
设抛物线的函数表达式为y=ax²+bx，
可得方程组

64a-8b=0 16a-4b=3

，
解得a=-

3

16

，b=-

3

2

，
∴y=-

3

16

x2-

3

2

x；
当OA=OB时，同理得y=-

3

4

x2-

15

4

x．

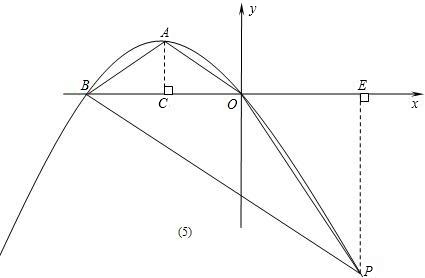
（3）当OA=AB时，若BP∥OA，如图（5），作PE⊥x轴，
则∠AOC=∠PBE，∠ACO=∠PEB=90°，
△AOC∽△PBE，

PE

BE

=

AC

OC

=

3

4

．
设BE=4m，PE=3m，则点P的坐标为（4m-8，-3m），
代入y=-

3

16

x2-

3

2

x，
解得m=3；
则点P的坐标为（4，-9），
S_梯形ABPO=S_△ABO+S_△BPO=48．
若OP∥AB，根据抛物线的对称性可得点P的坐标为（-12，-9），
S_梯形AOPB=S_△ABO+S_△BPO=48．


当OA=OB时，若BP∥OA，如图（6），作PF⊥x轴，
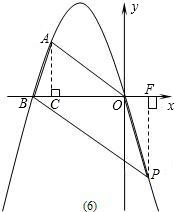
则∠AOC=∠PBF，∠ACO=∠PFB=90°，
△AOC∽△PBF，

PF

BF

=

AC

OC

=

3

4

；
设BF=4m，PF=3m，则点P的坐标为（4m-5，-3m），
代入y=-

3

4

x2-

15

4

x，
解得m=

3

2

．则点P的坐标为（1，-

9

2

），
S_梯形ABPO=S_△ABO+S_△BPO=

75

4

．
若OP∥AB（图略），作PF⊥x轴，
则∠ABC=∠POF，∠ACB=∠PFO=90°，
△ABC∽△POF，

PF

OF

=

AC

BC

=3；
设点P的坐标为（-n，-3n），
代入y=-

3

4

x2-

15

4

x，
解得n=9．
则点P的坐标为（-9，-27），S_梯形AOPB=S_△ABO+S_△BPO=75．

点评：此题考查了等腰三角形的判定、二次函数解析式的确定、梯形的判定、图形面积的求法等知识．同时还考查了分类讨论的数学思想，一定要考虑全面，避免漏解．