
分析 先设反比例函数的解析式y=$\frac{k}{x}$,根据甲同学说的可知k=±2016,根据乙同学说的可知k<0,综合可得k=-2016,即得到反比例函数的解析式.
解答 解:从这个反比例函数图象上任意一点向x轴、y轴作垂线,与两坐标轴所围成的矩形面积为2016,
|k|=|xy|=2016,
k=2016或k=-2016,
∵这个反比例函数在相同的象限内,y随着x增大而增大,
∴k=-2016,
故反比例函数的解析式是y=$y=-\frac{2016}{x}$.
故答案为:$y=-\frac{2016}{x}$.
点评 本题考查了反比例函数系数k的几何意义,先由面积求出|k|,再由反比例函数的性质求出k的值.


科目:初中数学 来源: 题型:解答题
 已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9.
已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是3$\sqrt{3}$.
如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点A(1,2)是反比例函数y=$\frac{k}{x}$图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是(-3,0)或(5,0)或(3,0)或(-5,0).
如图,已知点A(1,2)是反比例函数y=$\frac{k}{x}$图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是(-3,0)或(5,0)或(3,0)或(-5,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
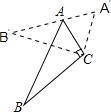 如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C′,且点A在A′B′上,则旋转角为50°.
如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C′,且点A在A′B′上,则旋转角为50°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com