
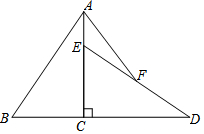
 如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )
如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )| A. | 4 | B. | 5 | C. | 4$\sqrt{2}$ | D. | 6 |
分析 取CE的中点G,连接FG.依据旋转的性质CE=BC=4,CD=AC=6,则AE=2,由G时CE的中点可求得AG=4,然后利用三角形的中位线定理可得到FG=3,最后在Rt△AFG中依据勾股定理求解即可.
解答 解:如图所示:取CE的中点G,连接FG.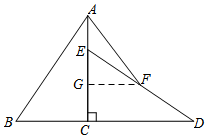
由旋转的性质可知:CE=BC=4,CD=AC=6,
∴AE=2,GE=2.
∴AG=4.
∵点G为CE的中,点F为ED的中点,
∴GF=$\frac{1}{2}$CD=3,GF∥CD.
又∵CD⊥AC,
∴FG⊥AC.
在Rt△AGF中,依据勾股定理可知AF=$\sqrt{A{G}^{2}+F{G}^{2}}$=5.
故选:B.
点评 本题主要考查的是旋转的性质、勾股定理的应用、三角形中位线的性质,掌握本题的辅助线的作法是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
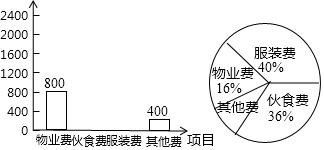
| 项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
| 金额/元 | 800 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
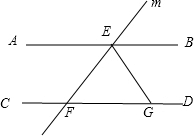 如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )
如图,已知直线AB∥CD,直线m与AB、CD相交于点E、F,EG平分∠FEB,∠EFG=50°,则∠FEG的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是104 | B. | 众数是103 | C. | 中位数是104 | D. | 方差是1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 地铁站 | A | B | C | D | E |
| x(千米) | 8 | 9 | 10 | 11.5 | 13 |
| y1(分钟) | 18 | 20 | 22 | 25 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com