
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图像与x轴交于点
的图像与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)在坐标系中能否找到点![]() ,使得
,使得![]() 且
且![]() ?如果能,求出满足条件的点
?如果能,求出满足条件的点![]() 的坐标;如果不能,请说明理由.
的坐标;如果不能,请说明理由.
【答案】(1)![]() ;(2)(3,3)或(1,-1)
;(2)(3,3)或(1,-1)
【解析】
(1)由待定系数法将点A,B的坐标代入即可求得;
(2)根据点P在线段AB的垂直平分线上,且点P到AB中点的距离等于AB的一半进行求解,构造全等三角形得到点P的坐标.
解:(1)∵直线AB经过点A(4,0),B(0,2)
代入y=kx+b中,得![]() ,
,
解得: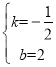 ,
,
∴AB的解析式为:![]() ;
;
(2)如图,点P在AB的垂直平分线上,且∠APB=90°,
可知△APB为等腰直角三角形,
过点P作y轴的垂线于点M,过A作MP的垂线于点N,
∵AB=![]() =
=![]() ,
,
∴BP=AP=![]() =
=![]() ,
,
∵∠MPB+∠APN=90°,∠APN+∠PAN=90°,
∴∠BPM=∠PAN,
在△PBM和△APN中,
 ,
,
∴△PBM≌△APN(AAS)
∴MB=PN,MP=AN,
设MB=x,则AN=MP=x+2,
∴在直角△MBP中,
MB2+MP2=BP2,
即![]() ,
,
解得:x=1,
∴MP=AN=3,
点P的坐标为(3,3),

同理:如图,当点P在直线AB下方时,
有△BMP≌△PNA(AAS),
设MP为y,则OM=AN=y,BM=4-y,
在直角△BMP中,
BM2+MP2=BP2,
即(2+y)2+y2=![]() ,
,
解得:y=1,
∴MP=1=OM,
即点P坐标为(1,-1)
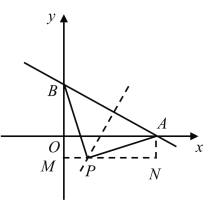
综上:能够找到点P满足条件,点P坐标为(3,3)或(1,-1).


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
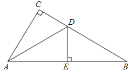
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
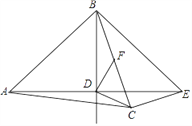
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像分别与
的图像分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,以线段
,以线段![]() 为边在第四象限内作等腰直角
为边在第四象限内作等腰直角![]() ,且
,且![]() .
.
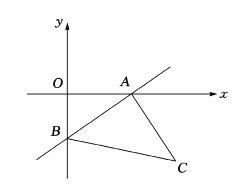
(1)试写出点![]() 的坐标:
的坐标: ![]() (_ _,_ ___),
(_ _,_ ___),![]() (_ ,_ )
(_ ,_ )
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的函数表达式
的函数表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②a+b+c>0;③方程ax2+bx+c=0的根是x1=﹣1,x2=3; ④b2﹣4ac>0;⑤当x>1时,y随x的增大而增大;正确的说法有( )
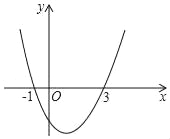
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,DE平分∠ADB,则∠B=( )
A. 40° B. 30° C. 25° D. 22.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=4,面积是16,AC的垂直平分线EF分别交AC,AB边于点E、F,若点D为BC边上的中点,点M为线段EF一动点,则△CDM周长的最小值为( )
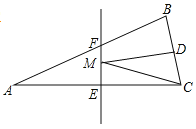
A.4B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com