
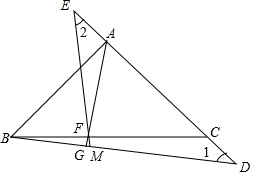
 等腰Rt△ABC中,AC=AB,∠BAC=90°,点D、E是AC上两点且AD=CE,AF⊥BD于点G,交BC于点F,连接EF交BD于点M,求证:∠1=∠2.
等腰Rt△ABC中,AC=AB,∠BAC=90°,点D、E是AC上两点且AD=CE,AF⊥BD于点G,交BC于点F,连接EF交BD于点M,求证:∠1=∠2. 分析 过A作AN⊥BC于N,延长AN交BD于H,根据等腰直角三角形的性质得到∠ABN=45°,AN=BN,根据三角形的内角和得到∠MBF=∠NAF,根据全等三角形的性质得到AF=BH,根据线段垂直平分线的性质得到BH=CH=AF,根据等腰三角形的性质得到∠HCN=∠HBN,∠NBA=∠NCA,等量代换得到∠HCA=∠HBA,推出△FAE≌△HCD,于是得到结论.
解答 证明: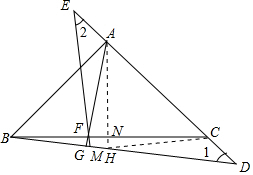 过A作AN⊥BC于N,延长AN交BD于H,
过A作AN⊥BC于N,延长AN交BD于H,
∵AN⊥BC,
∴∠ANB=90°,
∵△ABC是等腰直角三角形,
∴∠ABN=45°,
∴AN=BN.
∵AN是BC边上的高,由“三线合一”得∠NAB=∠ABC=45°,
∴∠NAF+∠FAB=45°,
∴AM⊥BD,
∴∠AGB=90°,
在Rt△ABG中,∠GBA+∠GAB=90°,∠MBF+∠FBA+∠GAB=90°,
∴∠MBF+∠FAB=45°,
∴MBF=NAF,
在△HNB和△FNA中,$\left\{\begin{array}{l}{∠NBH=∠NAF}\\{BN=AN}\\{∠BNH=∠ANF}\end{array}\right.$,
∴△HNB≌△FNA,
∴AF=BH,
∵AN⊥BC,N是BC中点,
∴AH是BC的垂直平分线,
∴BH=CH=AF,
∴∠HCN=∠HBN,∠NBA=∠NCA,
∴∠HCA=∠HBA,
∴∠HCA=45°+∠HBN,
∵△HNB≌△FNA,
∴∠HBN=∠FAN,
∴∠FAN+45°=∠HBN+45°,
∵∠NAC=45°,
∴∠FAC=∠ABN+45°,
∴∠FAC=∠HCA,
∵∠FAC+∠FAE=180°,∠HCA+∠HCD=180°,
∴∠HBN=∠FAE,
在△FAE与△HCD中,$\left\{\begin{array}{l}{HC=FA}\\{∠HCD=∠FAE}\\{CD=AE}\end{array}\right.$,
∴△FAE≌△HCD,
∴∠1=∠2.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,线段垂直平分线的性质,正确的作出辅助线是解题的关键.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:填空题
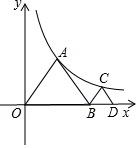 如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).
如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com