
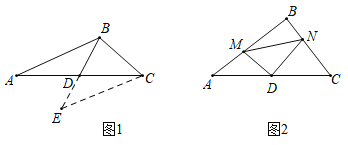
【题目】(1)阅读理解:如图1,在![]() 中,若
中,若![]() ,
,![]() .求
.求![]() 边上的中线
边上的中线![]() 的取值范围.小聪同学是这样思考的:延长
的取值范围.小聪同学是这样思考的:延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() .利用全等将边
.利用全等将边![]() 转化到
转化到![]() ,在
,在![]() 中利用三角形三边关系即可求出中线
中利用三角形三边关系即可求出中线![]() 的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线
的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线![]() 的取值范围是__________.
的取值范围是__________.
(2)问题解决:如图2,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,若
边上,若![]() .求证:
.求证:![]() .
.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】感恩节即将来临,小王调查了初三年级部分同学在感恩节当天将以何种方式对帮助过自己的人表达感谢,他将调查结果分为如下四类:A类﹣﹣当面表示感谢、B类﹣﹣打电话表示感谢、C类﹣﹣发短信表示感谢、D类﹣﹣写书信表示感谢.他将调查结果绘制成了如图所示的扇形统计图和条形统计图.请你根据图中提供的信息完成下列各题:
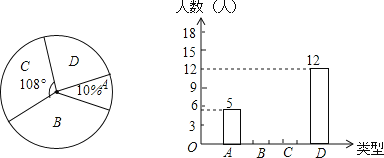
(1)补全条形统计图;
(2)在A类的同学中,有4人来自同一班级,其中有2人主持过班会.现准备从他们4人中随机抽出两位同学主持感恩节主题班会课,请用树状图或列表法求抽出1人主持过班会而另一人没主持过班会的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.

(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若Rt△AQP≌Rt△ACP≌Rt△BQP,求tanB的值;
(3)已知AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】统计七年级部分同学的跳高测试成绩,得到如下频率直方图(每组含前一个边界值,不含后一个边界值).

(1)参加测试的总人数是多少人?
(2)组距为多少?
(3)跳高成绩在![]() (含
(含![]() )以上的有多少人?占总人数的百分之几?
)以上的有多少人?占总人数的百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
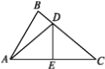
【题目】如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;

(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com