
【题目】已知,抛物线![]() ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线![]() (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线![]() 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)设抛物线的解析式为:![]() ,把h=1,k=2代入得到:
,把h=1,k=2代入得到:![]() .由抛物线过原点,得到
.由抛物线过原点,得到![]() ,从而得到结论;
,从而得到结论;
(2)由抛物线![]() 经过点A(h,k),得到
经过点A(h,k),得到![]() ,从而有
,从而有![]() ,由抛物线经过原点,得到
,由抛物线经过原点,得到![]() ,从而得到
,从而得到![]() ;
;
(3)由点A(h,k)在抛物线![]() 上,得到
上,得到![]() ,故
,故![]() ,由抛物线经过原点,得到
,由抛物线经过原点,得到![]() ,从而有
,从而有![]() ;然后分两种情况讨论:①当-2≤h<0时,②当0<h<1时.
;然后分两种情况讨论:①当-2≤h<0时,②当0<h<1时.
试题解析:(1)根据题意,设抛物线的解析式为:![]() (a≠0),∵h=1,k=2,∴
(a≠0),∵h=1,k=2,∴![]() .∵抛物线过原点,∴
.∵抛物线过原点,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() ;
;
(2)∵抛物线![]() 经过点A(h,k),∴
经过点A(h,k),∴![]() ,∴
,∴![]() ,∵抛物线经过原点,∴
,∵抛物线经过原点,∴![]() ,∵h≠0,∴
,∵h≠0,∴![]() ;
;
(3)∵点A(h,k)在抛物线![]() 上,∴
上,∴![]() ,∴
,∴![]() ,∵抛物线经过原点,∴
,∵抛物线经过原点,∴![]() ,∵h≠0,∴
,∵h≠0,∴![]() ;
;
分两种情况讨论:
①当-2≤h<0时,由反比例函数性质可知:![]() ,∴
,∴![]() ;
;
②当0<h<1时,由反比例函数性质可知:![]() ,∴
,∴![]() ;
;
综上所述,a的取值范围是![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中:
①若a+b+c=0,则 (a+c)2=b2.
②若a+b+c=0,则x=1一定是关于x的方程ax+b+c=0的解.
③若a+b+c=0,且abc≠0,则abc>0.
④若a+b+c=0,则 | a |=| b+c |.
其中正确的是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题中正确的是( )
①与圆有公共点的直线是该圆的切线;
②垂直于圆的半径的直线是该圆的切线;
③到圆心的距离等于半径的直线是该圆的切线;
④过圆直径的端点,垂直于此直径的直线是该圆的切线.
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把(a2+1)2-4a2分解因式得( )
A.(a2+1-4a)2B.(a2+1+2a)(a2+1-2a)
C.(a+1)2(a-1)2D.(a2-1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是![]() 的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.

(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
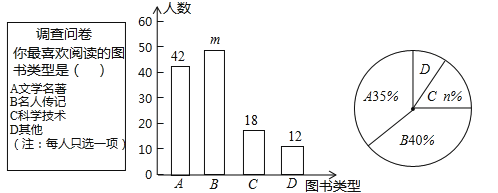
(1)本次调查共抽查了 名学生;
(2)两幅统计图中的m= ,n= .
(3)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com