
【题目】在△ABC和△DEF中,若∠A=∠D,则下列四个条件:①![]() =
=![]() ;②
;②![]() =
=![]() ;③∠B=∠F;④∠E=∠F中,一定能推得△ABC与△DEF相似的共有( )
;③∠B=∠F;④∠E=∠F中,一定能推得△ABC与△DEF相似的共有( )
A. 1个 B. 2个 C. 3个 D. 4个
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,点P为抛物线y=![]() x2上一动点.
x2上一动点.
(1)若抛物线y=![]() x2是由抛物线y=
x2是由抛物线y=![]() (x+2)2﹣1通过图象平移得到的,请写出平移的过程;
(x+2)2﹣1通过图象平移得到的,请写出平移的过程;
(2)若直线l经过y轴上一点N,且平行于x轴,点N的坐标为(0,﹣1),过点P作PM⊥l于M.
①问题探究:如图一,在对称轴上是否存在一定点F,使得PM=PF恒成立?若存在,求出点F的坐标:若不存在,请说明理由.
②问题解决:如图二,若点Q的坐标为(1.5),求QP+PF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 上
上![]() 点处,延长
点处,延长![]() ,
,![]() 交于点
交于点![]() .有下列四个结论:①
.有下列四个结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() .其中,将正确结论的序号全部选对的是( )
.其中,将正确结论的序号全部选对的是( )
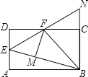
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E为BC边上的一点.连结AE.
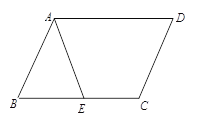
(1)若AB=AE, 求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF︰FA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
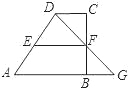
【题目】如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:△CDF∽△BGF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的有 ( )个
①40°角为内角的两个等腰三角形必相似
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为750
③一组对边平行,另一组对边相等的四边形是平行四边形
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1
⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A. 8:1B. 6:1C. 5:1D. 4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
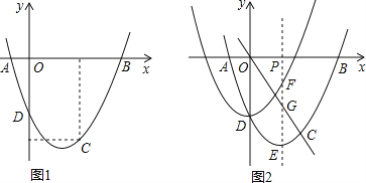
【题目】如图,抛物线y=![]() x2+bx+c经过A(-1,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
x2+bx+c经过A(-1,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
(1)求此抛物线的解析式及顶点坐标;
(2)若将此抛物线平移,使其顶点为点D,需如何平移?写出平移后抛物线的解析式;
(3)过点P(m,0)作x轴的垂线(1≤m≤2),分别交平移前后的抛物线于点E,F,交直线OC于点G,求证:PF=EG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com