
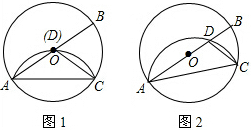
分析 (1)过点O作OE⊥AC于E,根据垂径定理可得AE=$\frac{1}{2}$AC,再根据翻折的性质可得OE=$\frac{1}{2}$r,然后在Rt△AOE中,利用勾股定理列式计算即可得解;
(2)连接BC,根据直径所对的圆周角是直角求出∠ACB,根据直角三角形两锐角互余求出∠B,再根据翻折的性质得到$\widehat{ADC}$所对的圆周角,然后根据∠ACD等于$\widehat{ADC}$所对的圆周角减去$\widehat{CD}$所对的圆周角,计算$\widehat{AD}$所对的圆心角的度数是80°,于是得到弧AD的长度=$\frac{80•π×4}{180}$=$\frac{16π}{9}$.
解答  解:(1)如图1,过点O作OE⊥AC于E,
解:(1)如图1,过点O作OE⊥AC于E,
则AE=$\frac{1}{2}$AC=$\frac{1}{2}$×2=1,
∵翻折后点D与圆心O重合,
∴OE=$\frac{1}{2}$r,
在Rt△AOE中,AO2=AE2+OE2,
即r2=12+($\frac{1}{2}$r)2,
解得r=$\frac{2\sqrt{3}}{3}$;
(2)连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°-∠BAC=90°-25°=65°,
根据翻折的性质,$\widehat{AC}$所对的圆周角为∠B,$\widehat{ABC}$所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB-∠A=65°-25°=40°,
∴$\widehat{AD}$所对的圆心角的度数是80°,
∴弧AD的长度=$\frac{80•π×4}{180}$=$\frac{16π}{9}$.
故答案为:$\frac{16π}{9}$.
点评 本题考查了垂径定理,勾股定理的应用,翻折的变换的性质,以及圆周角定理,(1)作辅助线构造出半径、半弦、弦心距为边的直角三角形是解题的关键,(2)根据同弧所对的圆周角相等求解是解题的关键.


科目:初中数学 来源: 题型:解答题
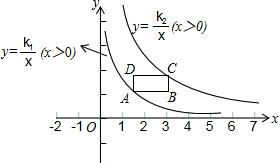 如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,点C在反比例函数L2:y=$\frac{{k}_{2}}{x}$(x>0)的图象上.
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,点C在反比例函数L2:y=$\frac{{k}_{2}}{x}$(x>0)的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
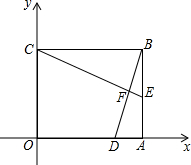 将一个矩形纸片如图所示放置在平面直角坐标系中,已知OB=5,OC=3,
将一个矩形纸片如图所示放置在平面直角坐标系中,已知OB=5,OC=3,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
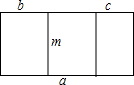 为扩大绿地面积,要把街心花园的一块长m米,宽a米,向两边分别加宽b米和c米.请你画出草图并用两种方法表示扩大后的绿地面积,思考这两种表示方法有何关系?
为扩大绿地面积,要把街心花园的一块长m米,宽a米,向两边分别加宽b米和c米.请你画出草图并用两种方法表示扩大后的绿地面积,思考这两种表示方法有何关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com