
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.

【答案】(1)证明见解析;(2)证明见解析;(3)DE=BE-AD.
【解析】试题分析:(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,推出∠ACD=∠CBE,根据AAS可得Rt△ADC≌Rt△CEB,得到AD=CE,CD=BE,即可求出答案;
(2)与(1)证法类似可证出∠ACD=∠CBE,能推出△ADC≌△CEB,得到AD=CE,CD=BE,根据线段的和差即可得到答案;
(3)同前两问可得△ACD≌△CBE,得到AD=CE,CD=BE,根据线段的和差即可得出结论.
试题解析:
证明:(1)∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC与△CEB中,
∠ADC=∠CEB,∠ACD=∠CBE,AC=CB,
∴Rt△ADC≌Rt△CEB (AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)∵∠ACB=∠CEB=90°,
∴∠ACD+∠ECB=∠CBE+∠ECB=90°,
∴∠ACD=∠CBE
在△ADC与△CEB中,
∠ADC=∠CEB=90°,∠ACD=∠CBE,AC=CB,
∴△ADC≌△CEB (AAS),
∴AD=CE,DC=BE,
∴DE=CE-CD=AD-BE;
(3)DE=BE-AD.
理由:同(1)(2)证法可得△ADC≌△CEB ,
∴AD=CE,DC=BE,
∴DE=CD-CE=BE-AD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我区正在实施的“同城一体化”工程进展顺利区招投标中心在对观光路工程招标时,接到甲、乙两个工程队的投标书,甲、乙施工一天的工程费用分别为1.5万元和1.1万元,区招投标中心根据甲、乙两队的投标书测算,应有三种施工方案:
(1)甲队单独做这项工程刚好如期完成;
(2)乙队单独做这项工程,要比规定日期多5天;
(3)若甲、乙两队合作4天后,余下的工程由乙队单独做,也正好如期完成.
在确保如期完成的情况下,你认为哪种方案最节省工程款,通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点分别为A(-2,3),B(-3,2),C(-1,1)
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)请在x轴上确定一点D,使点D到B、C的距离相等(要求用直尺和圆规作图,并保留作图痕迹)
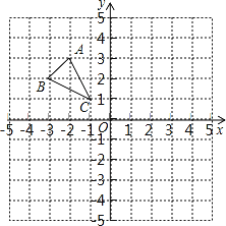
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.
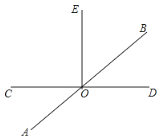
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)中日钓鱼岛争端持续,我海监船加大钓鱼岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.

(1)请用直尺和圆规作出C处的位置;
(2)求我国海监船行驶的航程BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)若∠DBC=25°,求∠ADC′的度数;
(2)若AB=4,AD=8,求△BDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com