
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ②③④ |
分析 分别利用三角形内切圆的性质以及多边形内角和定理以及中点四边形的性质和平行四边形的判定方法分析得出答案.
解答 解:①三角形有且只有一个内切圆,正确;
②四边形的内角和与外角和相等,正确;
③顺次连接四边形各边中点所得的四边形一定是平行四边形,故此选项错误;
④一组对边平行且一组对角相等的四边形是平行四边形,正确,
理由:连接BD,
∵AB∥CD,
∴∠ABD=∠CDB,
在△ABD和△CDB中,
$\left\{\begin{array}{l}{BD=DB}\\{∠ABD=∠CDB}\\{AB=CD}\end{array}\right.$,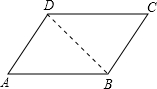
∴△ABD≌△CDB(SAS),
∴∠ADB=∠CBD,
∴AD∥BC.
又AB∥CD,
∴四边形ABCD是平行四边形.
故正确的有:①②④.
故选:C.
点评 此题主要考查了命题与定理,正确把握中点四边形以及平行四边形的判定方法是解题关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 篮球队员身高的中位数一定大于1.82米 | |
| B. | 篮球队员身高的众数一定小于1.82米 | |
| C. | 篮球队中比小亮高的队员不会超过5人 | |
| D. | 篮球队员身高的中位数与众数有可能相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.16 | B. | 2.15 | C. | 2.14 | D. | 2.13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x≥$\frac{1}{3}$ | D. | x≥-$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
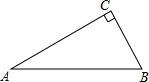 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com