
【题目】己知:![]() 为等边三角形,点E为射线AC上一点,点D为射线CB上一点,
为等边三角形,点E为射线AC上一点,点D为射线CB上一点,![]() .
.
(1)如图1,当E在AC的延长线上且![]() 时,AD是
时,AD是![]() 的中线吗?请说明理由;
的中线吗?请说明理由;
(2)如图2,当E在AC的延长线上时,![]() 等于AE吗?请说明理由;
等于AE吗?请说明理由;
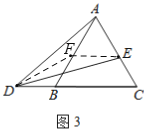
(3)如图3,当D在线段CB的延长线上,E在线段AC上时,请直接写出AB、BD、AE的数量关系.

【答案】(1)是,理由见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)由等边三角形的性质得∠BAC=∠ACD=60°,由等腰三角形的性质得∠CDE=∠E,再根据三角形外角的性质可得∠E=30°,继而可得 ∠DAC=∠E=30°,得出AD平分∠BAC,由此即可得AD是△ABC的中线;
(2)在AB上取BH=BD,连接DH,利用AHD≌△DCE得出DH=CE,得出AE=AB+BD,
(3)在AB上取AF=AE,连接DF,利用△AFD≌△EFD得出角的关系,得出△BDF是等腰三角形,根据边的关系得出结论AB-BD=AE.
(1)是,理由如下:
∵△ABC是等边三角形,
∴∠BAC=∠ACD=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACD=∠E+∠CDE,
∴∠E=30°,
∵AD=DE,
∴∠DAC=∠E=30°,
∴∠DAC=![]() ∠BAC,
∠BAC,
即AD平分∠BAC,
∴AD是△ABC的中线;
(2)![]() ,理由如下:
,理由如下:
如图2,在AB上取BH=BD,连接DH,
∵△ABC是等边三角形,
∴∠BAC=∠ACD=∠B=60°,AB=AC,
∴∠DCE=120°,△BDH是等边三角形,
∴DH=BD,∠DHB=60°,
∴∠AHD=120°,∠DHB=∠CAB,
∴∠DCE=∠AHD,DH//AC,
∵AD=DE,
∴∠E=∠DAC,
∵DH//AC,
∴∠HAD=∠DAC,
∴∠HAD=∠E,
∴△ADH≌△DEC,
∴DH=CE,
∴CE=BD,
∴AB+BD=AC+CE=AE;

(3)AE=AB-BD,理由如下:
如图3,在AB上取AF=AE,连接DF,EF,
∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴△AEF是等边三角形,
∴AF=EF,∠AFE=∠AFE=∠FAE=60°,
∴∠AFE=∠ABC,
∴EF//BC,
∴∠FED=∠EDB,
∵AD=DE,DF=DF,AF=EF,
∴△ADF≌△EDF,
∴∠DAF=∠DEF,∠ADF=∠EDF,
∵∠DFB=∠DAF+∠ADF,∠FDB=∠EDF+EDB,
∴∠DFB=∠FDB,
∴BD=BF,
∵AB-BF=AF,
∴AB-BD=AE.


科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系
在平面直角坐标系![]() 中,
中,
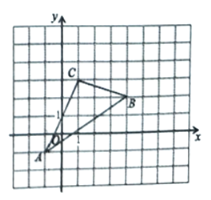
(1)请直接写出![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若把![]() 向上平移
向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位得
个单位得![]() ,请在图中画出
,请在图中画出![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(3)求![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为
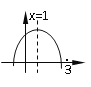
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
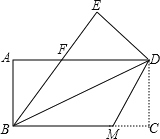
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
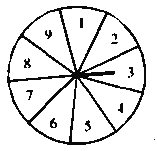
【题目】如图,一个均匀的转盘被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
小亮和小芳两人玩转盘游戏,对游戏规则,小芳提议:若转岀的数字是3的倍数,小芳获胜,若转出的数字是4的倍数,小亮获胜.
(1)你认为小芳的提议合理吗?为什么?
(2)利用这个转盘,请你为他俩设计一种对两人都公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由正比例函数![]() 沿
沿![]() 轴的正方向平移4个单位而成的一次函数
轴的正方向平移4个单位而成的一次函数![]()
的图像与反比例函数![]() (
(![]() )在第一象限的图像交于A(1,n)和B两点.
)在第一象限的图像交于A(1,n)和B两点.
(1)求一次函数![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)求△ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的部分。
抽样调查学生最喜欢的体育活动人数的直方图 抽样调查学生最喜欢的体育活动人数扇形统计图.

请根据以上信息解答以下问题:
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据,②图2中![]() =________;
=________;
(3)若该校共有学生800人,请你估计该校最喜羽毛球项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com