
【题目】在平面直角坐标系 xOy 中,抛物线 y mx![]() 2mx 3与 y 轴交于点C ,该抛物线对称轴与 x 轴的交于点 A.
2mx 3与 y 轴交于点C ,该抛物线对称轴与 x 轴的交于点 A.
(1)求该抛物线的对称轴及点 A 、C 的坐标;
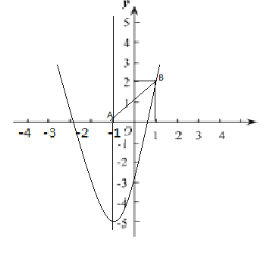
(2)点 A 向右移动两个单位长度,向上移动两个单位长度,得到点 B,若抛物线与线段 AB恰有一个交点时,结合图象,求 m 的取值范围.
【答案】(1)对称轴![]() ,
,![]() ,
,
(2)![]() 或
或![]() .
.
【解析】
(1)由![]() 轴上的点横坐标为0,可得C的坐标,由抛物线的对称轴公式求对称轴,再可以求A的坐标.
轴上的点横坐标为0,可得C的坐标,由抛物线的对称轴公式求对称轴,再可以求A的坐标.
(2)利用函数过定点C,分![]() 分别画出函数的大致图像,观察图像与线段AB,找到满足一个交点的条件即可得到答案.
分别画出函数的大致图像,观察图像与线段AB,找到满足一个交点的条件即可得到答案.
解:(1)由抛物线的对称轴为:![]() ,
,
所以对称轴为![]() ,
,
令![]() ,得
,得![]() ,所以抛物线与
,所以抛物线与![]() 轴的交点C的坐标为(0,-3)
轴的交点C的坐标为(0,-3)
因为抛物线的对称轴![]() 与
与![]() 轴交于点A,所以A(-1,0)
轴交于点A,所以A(-1,0)
所以:抛物线的对称轴为![]() ,A(-1,0),C(0,-3).
,A(-1,0),C(0,-3).
(2)点A(-1,0) 向右移动两个单位长度,向上移动两个单位长度,得到点 B,
所以B(1,2),因为抛物线![]() 过C(0,-3),
过C(0,-3),
当![]() >0,抛物线开口向上,把B(1,2)代入解析式得:
>0,抛物线开口向上,把B(1,2)代入解析式得:![]() ,
,
所以![]() ,
,
由![]() 越大,抛物线的开口越窄,当抛物线与线段AB恰好有一个交点时,
越大,抛物线的开口越窄,当抛物线与线段AB恰好有一个交点时,![]() .
.
当![]() <0,抛物线开口向下,把A(-1,0)代入解析式得:
<0,抛物线开口向下,把A(-1,0)代入解析式得:![]() ,
,
所以![]() ,
,
当抛物线与线段AB恰好有一个交点时,由抛物线的顶点![]() 得;
得;
![]() .所以
.所以![]() .
.
综上:![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
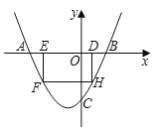
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011广西崇左,18,3分)已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )
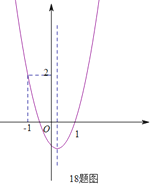
A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校共有六个年级,每个年级 10 个班,每个班约 40 名同学.该校食堂共有 10 个窗口中午所有同学都在食堂用餐.经了解,该校同学年龄分布在 12 岁(含 12 岁)到 18岁(含 18 岁)之间,平均年龄 15 岁.小天、小东两位同学,为了解全校同学对食堂各窗口餐食的喜爱情况,各自进行了抽样调查,并记录了相应同学的年龄,每人调查了 60 名同学,将收集到的数据进行了整理.
小天从初一年级每个班随机抽取 6 名同学进行调查,绘制统计图表如下:

小东从全校每个班随机抽取 1 名同学进行调查,绘制统计图表如下:

根据以上材料回答问题:
(1)写出图 2 中 m 的值 ;
(2)小天、小东两人中,哪个同学抽样调查的数据能较好地反映出该校同学对各窗口餐食的喜爱情况,并简要说明另一名同学调查的不足之处;
(3)为使每个同学在中午尽量吃到自己喜爱的餐食,学校餐食管理部门应为 窗口尽 量多的分配工作人员,理由为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,CD为中线,点Q在线段CD上运动,将线段QA绕点Q顺时针旋转,使得点A的对应点E落在射线BC上,连接BQ,设∠DAQ=α(0°<α<60°且α≠30°).
(1)当0°<α<30°时,
①在图1中依题意画出图形,并求∠BQE(用含α的式子表示);
②探究线段CE,AC,CQ之间的数量关系,并加以证明;
(2)当30°<α<60°时,直接写出线段CE,AC,CQ之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次羽毛球赛中,甲运动员在离地面![]() 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).
米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).

(1)求抛物线的解析式(不要求写自变量的取值范围);
(2)求羽毛球落地点N离球网的水平距离(即NC的长);
(3)乙原地起跳后可接球的最大高度为2.4米,若乙因为接球高度不够而失球,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com