
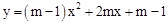 .
.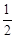 ;(2)m<
;(2)m<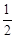 ;(3)
;(3)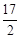 .
.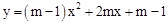 图象与x轴只有一个交点,
图象与x轴只有一个交点,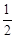 .
.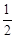 .
.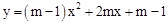 ,
,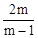 ,ab=1,
,ab=1,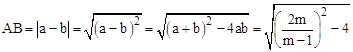 .
.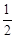 AB•yC纵坐标=4,即|m-1|×
AB•yC纵坐标=4,即|m-1|×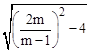 =8,
=8,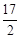 .
.

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,抛物线
中,抛物线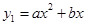 过点A(6,0)和点B(3,
过点A(6,0)和点B(3, ).
).
 的解析式;
的解析式; 沿x轴翻折得抛物线
沿x轴翻折得抛物线 ,求抛物线
,求抛物线 的解析式;
的解析式; 上是否存在点M,使
上是否存在点M,使 与
与 相似?如果存在,求出点M的坐标;如果不存在,说明理由.
相似?如果存在,求出点M的坐标;如果不存在,说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 Rt
Rt (
( )的直角边与正方形
)的直角边与正方形 的边长均为2,且
的边长均为2,且 与
与 在同一直线上,开始时点
在同一直线上,开始时点 与点
与点 重合,让
重合,让 沿这条直线向右平移,直到点
沿这条直线向右平移,直到点 与点
与点 重合为止.设
重合为止.设 的长为
的长为 ,
, 与正方形
与正方形 重合部分(图中阴影部分)的面积为
重合部分(图中阴影部分)的面积为 ,则
,则 与
与 之间的函数关系的图象大致是( )
之间的函数关系的图象大致是( )

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com