
分析 过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,由题意可得:OA=OC=3,AF=FB=1,CE=ED=2,E、F、O在一条直线上,EF为AB、CD之间的距离,再分别解Rt△OEC、Rt△OFA,即可得OE、OF的长,然后分AB、CD在圆心的同侧和异侧两种情况求得AB与CD的距离.
解答  解:①当AB、CD在圆心两侧时;
解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=3,弦AB∥CD,且AB=2,CD=4,
∴OA=OC=3,CE=DE=2,AF=FB=1,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2-CE2
∴OE=$\sqrt{{OC}^{2}-{CE}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
在Rt△OFA中,由勾股定理可得:
OF2=OA2-AF2
∴OF=$\sqrt{{OA}^{2}-{AF}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
∴EF=OE+OF=$\sqrt{5}$+2$\sqrt{2}$,即b=2$\sqrt{2}$+$\sqrt{5}$
②当AB、CD在圆心同侧时;
同①可得:OE=$\sqrt{5}$,OF=2$\sqrt{2}$;
则AB与CD的距离为:OF-OE=2$\sqrt{2}$-$\sqrt{5}$,即d=2$\sqrt{2}$-$\sqrt{5}$;
故答案为:2$\sqrt{2}$±$\sqrt{5}$.
点评 本题考查的是垂径定理,在解答此题时要进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 印制x(张) | … | 100 | 200 | 300 | … |
| 收费y(元) | … | 1 | 30 | 45 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
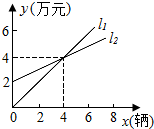 如图,l1表示信达商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系,观察图象,解决以下问题:
如图,l1表示信达商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系,观察图象,解决以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com