
 口算题天天练系列答案
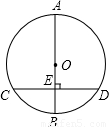
口算题天天练系列答案科目:初中数学 来源:2000年全国中考数学试题汇编《二次函数》(03)(解析版) 题型:解答题
查看答案和解析>>
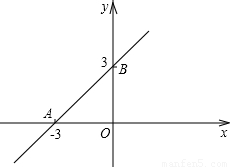
科目:初中数学 来源:2000年北京市东城区中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
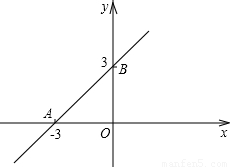
科目:初中数学 来源:2000年全国中考数学试题汇编《数据收集与处理》(01)(解析版) 题型:解答题
 (2000•东城区)附加题:为保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克;第二天收集1号电池2节,5号电池3节,总重量为240克.
(2000•东城区)附加题:为保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克;第二天收集1号电池2节,5号电池3节,总重量为240克.| 1号电池(单位:节) | 29 | 30 | 32 | 28 | 31 |
| 5号电池(单位:节) | 51 | 53 | 47 | 49 | 50 |
查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《锐角三角函数》(01)(解析版) 题型:选择题
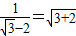

查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《锐角三角函数》(01)(解析版) 题型:选择题
 ,那么cos(90°-α)的值是( )
,那么cos(90°-α)的值是( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com