Question

20．如图，在平面直角坐标系中，矩形OABC的边OA=2，OC=6，在OC上取点D将△AOD沿AD翻折，使O点落在AB边上的E点处，将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动，且一直角边始终经过点D，另一直角边所在直线与直线DE，BC分别交于点M，N．
（1）填空：经过A，B，D三点的抛物线的解析式是y=-$\frac{1}{4}$x²-$\frac{3}{2}$x-2；
（2）已知点F在（1）中的抛物线的对称轴上，求点F到点B，D的距离之差的最大值；
（3）如图1，当点P在线段DA上移动时，是否存在这样的点M，使△CMN为等腰三角形？若存在，请求出M点坐标；若不存在，请说明理由；
（4）如图2，当点P在线段AB上移动时，设P点坐标为（x，-2），记△DBN的面积为S，请直接写出S与x之间的函数关系式，并求出S随x增大而增大时所对应的自变量x的取值范围．

Answer 1

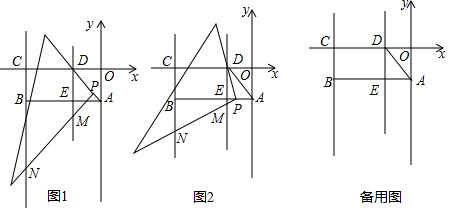
分析 （1）根据△AOD沿AD翻折，使O点落在AB边上的E点处，得到∠OAD=∠EAD=45°，DE=OD，求出OD=2，得出D点的坐标，再根据DE=OD=2，求出D点的坐标；把A，B，D三点分别代入抛物线解析式，求得系数的值即可；
（2）由轴对称的性质得到FA=FB，|FB-FD|=|FA-FD|≤AD=2$\sqrt{2}$，即点F到点B，D的距离之差的最大值是2$\sqrt{2}$；
（3）由翻折可知四边形AODE为正方形，过M作MH⊥BC于H，先求出∠NMH=∠MNH=45°，得出NH=MH=4，MN=4$\sqrt{2}$，再根据直线OE的解析式为：y=x，依题意得MN∥OE，设MN的解析式为y=x+b，根据DE的解析式为x=2，BC的解析式为x=6，得出M（2，2+b），N（6，6+b），CM=$\sqrt{{4}^{2}+（2+b）^{2}}$，CN=6+b，MN=4$\sqrt{2}$，①当CM=CN时，4²+（2+b）²=（6+b）²，解得：b=-2，此时M（2，0）；②当CM=MN时，4²+（2+b）²=（4$\sqrt{2}$）²，解得：b₁=2，b₁=-6（不合题意舍去），此时M（2，4）；③当CM=MN时，6+b=4$\sqrt{2}$，解得：b=4$\sqrt{2}$-6，此时M（2，4$\sqrt{2}$-4）；
（4）根据题意先证出△PBN∽△DEP，得出BN的值，求出S与x之间的函数关系式，根据①当0≤x≤2时，S=x²-8x+12=（x-4）²-4，②当2＜x≤6时，S=-x²+8x-12=-（x-4）²+4，即可得出答案．

解答 解：（1）设抛物线解析式为y=ax²+bx+c（a≠0），
∵将△AOD沿AD翻折，使O点落在AB边上的E点处，
∴∠OAD=∠EAD=45°，DE=OD，
∴OA=OD，
∵OA=2，
∴OD=2，
∴D点坐标是（2，0），
把A（0，-2），B（-6，-2），D（2，0）分别代入y=ax²+bx+c（a≠0），得
$\left\{\begin{array}{l}{c=-2}\\{36a-6b+c=-2}\\{4a+2b+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=-\frac{3}{2}}\\{c=-2}\end{array}\right.$，
故抛物线解析式为：y=-$\frac{1}{4}$x²-$\frac{3}{2}$x-2．
故答案是：y=-$\frac{1}{4}$x²-$\frac{3}{2}$x-2；

（2）∵点A，B关于抛物线的对称轴对称，
∴FA=FB，
∴|FB-FD|=|FA-FD|，
∵|FA-FD|≤AD=2$\sqrt{2}$，
∴点F到点B，D的距离之差的最大值是2$\sqrt{2}$；
（3）存在点M使△CMN为等腰三角形，理由如下：
由翻折可知四边形AODE为正方形，过M作MH⊥BC于H，
∵∠PDM=∠PMD=45°，则∠NMH=∠MNH=45°，NH=MH=4，MN=4$\sqrt{2}$，
∵直线OE的解析式为：y=x，依题意得MN∥OE，∴设MN的解析式为y=x+b，
而DE的解析式为x=-2，BC的解析式为x=-6，
∴M（-2，-2+b），N（-6，-6+b），CM²=4²+（-2+b）²，CN²=（-6+b）²，MN²=（4$\sqrt{2}$）²=32，
①当CM=CN时，4²+（-2+b）²=（-6+b）²，解得：b=2，此时M（-2，0）；
②当CM=MN时，4²+（-2+b）²=32，解得：b₁=-2，b₂=6（不合题意舍去），此时M（-2，-4）；
③当CN=MN时，6-b=4$\sqrt{2}$，解得：b=-4$\sqrt{2}$+6，此时M（-2，4-4$\sqrt{2}$）；
综上所述，使△CMN为等腰三角形的M点的坐标为：（-2，0），（-2，-4），（-2，4-4$\sqrt{2}$）；

（4）当-2≤x≤0时，∵∠BPN+∠DPE=90°，∠BPN+∠BNP=90°，
∴∠DPE=∠BNP，又∠PED=∠NBP=90°，
∴△DEP∽△PBN，
∴$\frac{PB}{DE}$=$\frac{BN}{EP}$，
∴$\frac{6+x}{2}$=$\frac{BN}{2+x}$，
∴BN=$\frac{（2+x）（6+x）}{2}$，
∴S_△DBN=$\frac{1}{2}$BN×BE=$\frac{1}{2}$×$\frac{（2+x）（6+x）}{2}$×4，整理得：S=x²+8x+12；
当-6≤x＜-2时，
∵△PBN∽△DEP，
∴$\frac{PE}{BN}$=$\frac{DE}{PB}$，
∴$\frac{2-x}{BN}$=$\frac{2}{x-6}$，
∴BN=$\frac{（2-x）（x+6）}{2}$，
∴S_△DBN=$\frac{1}{2}$BN×BE=$\frac{1}{2}$×$\frac{（-2-x）（x+6）}{2}$×4，整理得：S=-x²-8x-12；
则S与x之间的函数关系式：S=$\left\{\begin{array}{l}{{x}^{2}+8x+12（-2≤x≤0）}\\{-{x}^{2}-8x-12（-6≤x≤-2）}\end{array}\right.$，
①当-2≤x≤0时，S=x²+8x+12=（x+4）²-4，当x≥-4时，S随x的增大而增大，即-2≤x≤0，
②当-6≤x＜-2时，S=-x²-8x-12=-（x+4）²+4，当x≤-4时，S随x的增大而增大，即-6≤x≤-4，
综上所述：S随x增大而增大时，-2≤x≤0或-6≤x≤-4．

点评 此题考查了二次函数的综合，用到的知识点是勾股定理、一次函数、二次函数的图象与性质、轴对称等，关键是综合运用有关知识求出点的坐标，是一道综合题．