

分析 (1)过点G作GE∥AB,根据AB∥CD得出AB∥CD∥GE,再由平行线的性质即可得出结论;
(2)设FG与NE交点为H点,AB与NE的交点I,点在△HNG中由三角形内角和定理可知∠G+∠HNG+∠NHG=180°,再由MF平分∠AME,NE平分∠CNG,2∠E+∠G=90°可得出90°+$\frac{3}{2}$∠AME=180°,由此可得出结论;
(3)根据PQ平分∠MPN,NH平分∠PNC可得出∠JPQ=∠JPN-$\frac{1}{2}$∠MPN,由此得出结论.
解答  (1)证明:如图①,过点G作GE∥AB,
(1)证明:如图①,过点G作GE∥AB,
∵AB∥CD,
∴AB∥CD∥GE,
∴∠AMG=∠MGE,∠CNG=∠NGE,
∴∠AMG+∠CNG=∠MGN;
(2)如图②,设FG与NE交点为H点,AB与NE的交点I,
在△HNG中,
∵∠G+∠HNG+∠NHG=180° 
∴∠HNG=∠AIE=∠IHM+∠IMH=(∠E+∠EMF)+∠IMH=∠E+(∠EMF+∠IMH )=∠E+∠AME
∠NHG=∠IHM=∠E+∠EMF=∠E+$\frac{1}{2}$∠AME
∴∠G+∠HNG+∠NHG=∠G+(∠E+∠AME)+(∠E+$\frac{1}{2}$∠AME)=180° (∠G+2∠E)+$\frac{3}{2}$∠AME=180°,即90°+$\frac{3}{2}$∠AME=180°,
∴∠AME=60°;
(3)∵PQ平分∠MPN,NH平分∠PNC,
∴∠JPQ=∠JPN-$\frac{1}{2}$∠MPN
=$\frac{1}{2}$(∠ENC-$\frac{1}{2}$∠MPN)
=$\frac{1}{2}$(∠AOE-$\frac{1}{2}$∠MPN)
=$\frac{1}{2}$∠AME
=30°.
点评 本题考查的是平行线的性质,涉及到三角形外角的性质、角平分线的性质及三角形内角和定理,难度较大.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
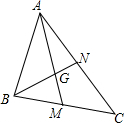 如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).
如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
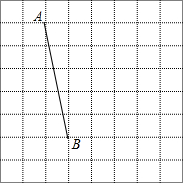 如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.
如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,已知∠C=90°,边AC=4cm,BC=5cm,点P为CB边上一点,当动点P沿CB从点C向点B运动时,△APC的面积发生了变化.
如图,在Rt△ABC中,已知∠C=90°,边AC=4cm,BC=5cm,点P为CB边上一点,当动点P沿CB从点C向点B运动时,△APC的面积发生了变化.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com