
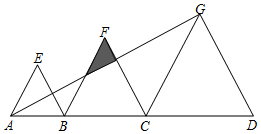
 如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则分析 ①利用相似三角形对应边成比例列式计算即可得解;
②设AG与CF、BF分别相交于点M、N,根据等边对等角求出∠CAG=∠CGA,再利用三角形的一个外角等于与它不相邻的两个内角的和求出∠CGA=30°,然后求出AG⊥GD,再根据相似三角形对应边成比例求出CM,从而得到MF,然后求出MN,再利用三角形的面积公式列式计算即可得解.
解答 ①解:∵△ABE、△CDG都是等边三角形,
∴△ABE∽△CDG,
∴$\frac{AB}{CD}$=$\frac{2}{5}$,
即$\frac{4}{CD}$=$\frac{2}{5}$,
解得CD=10;
②解:如图,设AG与CF、BF分别相交于点M、N,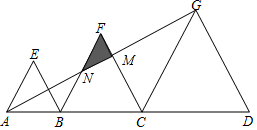
∵AC=AB+BC=4+6=10,
∴AC=CG,
∴∠CAG=∠CGA,
又∵∠CAG+∠CGA=∠DCG=60°,
∴∠CGA=30°,
∴∠AGD=∠CGA+∠CGD=30°+60°=90°,
∴AG⊥GD,
∵∠BCF=∠D=60°,
∴CF∥DG,
∴△ACM∽△ADG,
∴MN⊥CF,
$\frac{CM}{DG}$=$\frac{AC}{AD}$,
即$\frac{CM}{10}$=$\frac{10}{20}$,
解得CM=5,
所以,MF=CF-CM=6-5=1,
∵∠F=60°,
∴MN=$\sqrt{3}$MF=$\sqrt{3}$,
∴S△MNF=$\frac{1}{2}$MF•MN=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
即阴影部分面积为$\frac{\sqrt{3}}{2}$.
故答案为:10;$\frac{\sqrt{3}}{2}$.
点评 本题考查了相似三角线的判定与性质等边三角形的性质,主要利用了相似三角形对应边成比例的性质,难点在于②判断出直角三角形.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.
如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com