
【题目】已知,如图,在△ABC中,∠B <∠C,AD,AE分别是△ABC的高和角平分线。
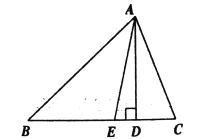
(1)若∠B=30°,∠C=50°,试确定∠DAE的度数;
(2)试写出∠DAE,∠B,∠C的数量关系,并证明你的结论。
【答案】(1)10°;(2)![]() (∠C-∠B)(或
(∠C-∠B)(或![]() ∠C-
∠C-![]() ∠B),理由见解析
∠B),理由见解析
【解析】(1)在三角形ABC中,由∠B与∠C的度数求出∠BAC的度数,根据AE为角平分线求出∠BAE的度数,由∠BAD-∠B即可求出∠DAE的度数;
(2)仿照(1)得出∠DAE与、∠B、∠C的数量关系即可.
解:(1)在△ABC中,
∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=180°-30°-50°=100°,
又∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=50°,
∠BAC=50°,
∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=180°-∠B-∠BDA=180°-30°-90°=60°,
∴∠DAE=∠BAD-∠BAE=60°-50°=10° ;
(2)∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=180°-∠B-∠BDA=180°-∠B-90°=90°-∠B,
又∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC,
∠BAC,
∴∠DAE=∠BAD-∠BAE=90°-∠B-![]() ∠BAC,
∠BAC,
=90°-∠B-![]() (180°-∠B-∠C),
(180°-∠B-∠C),
=![]() (∠C-∠B)(或
(∠C-∠B)(或![]() ∠C-
∠C-![]() ∠B).
∠B).


科目:初中数学 来源: 题型:
【题目】在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是![]() ”,小明做了下列三个模拟实验来验证.
”,小明做了下列三个模拟实验来验证.
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值. 上面的实验中,不科学的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
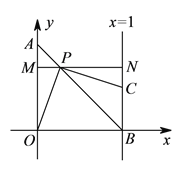
【题目】如图,以![]() 为原点的直角坐标系中,
为原点的直角坐标系中,![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 为线段
为线段![]() 上一动点,作直线
上一动点,作直线![]() ,交直线
,交直线![]() 于点
于点![]() .过
.过![]() 点作直线
点作直线![]() 平行于
平行于![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .记
.记![]() ,
,![]() 的面积为
的面积为![]() .
.
(![]() )当点
)当点![]() 在第一象限时:求证:
在第一象限时:求证:![]() ≌
≌![]() .
.
(![]() )当点
)当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 也随之在直线
也随之在直线![]() 上移动,求出
上移动,求出![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围.
之间的函数关系式,并写出自变量的取值范围.
(![]() )当点
)当点![]() 在线段
在线段![]() 上移动时,
上移动时,![]() 是否可能成为等腰三角形?如果可能,直接写出所有能使
是否可能成为等腰三角形?如果可能,直接写出所有能使![]() 成为等腰三角形的
成为等腰三角形的![]() 的值;如果不可能,请说明理由.
的值;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了全班本学期阅读课外书的情况,并根据统计数据,绘制如下的频率分布折线图和扇形统计图。
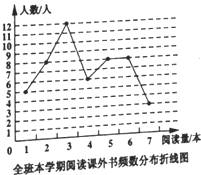
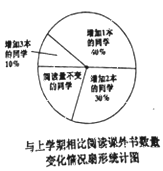
根据以上信息,回答下列问题:
①这个班共有__________ 名学生,本学期阅读量5本的有________ 人
②这个班本学期阅读量的中位数是_______ 本,众数是 ______ 本;
③求全班本学期比上学期每名同学的平均阅读量增加了多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
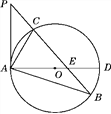
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:某学校在筹建数学实验室过程中,准备购进一批桌椅,现有三种桌椅可供选择:甲种每套150元,乙种每套210元,丙种每套250元。若该学校同时购买其中两种不同型号的桌椅50套,恰好花费了9000元,则共有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
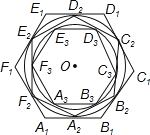
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
查看答案和解析>>
科目:初中数学 来源: 题型:
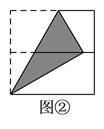
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com