




 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:阅读理解
| PG |
| PC |
| PG |
| PC |
 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出| PG |
| PC |
查看答案和解析>>
科目:初中数学 来源:江苏省镇江市实验初中2011-2012学年七年级下学期期中考试数学试题 题型:044
阅读并探究下列问题:

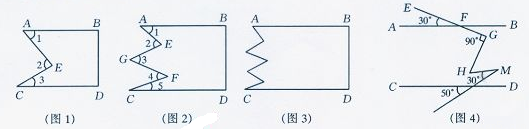
(1)如图1,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?为什么?
(2)如图2,将长方形纸片剪四刀,其中AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?为什么?
(3)如图3,将长方形纸片剪n刀,其中AB∥CD,你又有何发现?(用简洁的语言表述)
(4)如图4,直线AB∥CD,∠EFD=30°,∠GHK=35°,∠HKG=40°,∠AGM=50°,则∠FGH=________.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年安徽马鞍山七年级下期末数学试卷(带解析) 题型:解答题
阅读并探究下列问题:
(1)如图1,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?为什么?
(2)如图2,将长方形纸片剪四刀,其中AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?为什么?
(3)如图3,将长方形纸片剪n刀,其中AB∥CD,你又有何发现?
(4)如图4,直线AB∥CD,∠EFA=30.,∠FGH=90.,∠HMN=30.,∠CNP=50.,
则∠GHM= .
查看答案和解析>>
科目:初中数学 来源:2014届安徽马鞍山七年级下期末数学试卷(解析版) 题型:解答题
阅读并探究下列问题:
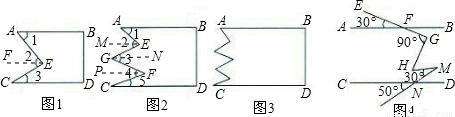
(1)如图1,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?为什么?
(2)如图2,将长方形纸片剪四刀,其中AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?为什么?
(3)如图3,将长方形纸片剪n刀,其中AB∥CD,你又有何发现?
(4)如图4,直线AB∥CD,∠EFA=30.,∠FGH=90.,∠HMN=30.,∠CNP=50.,
则∠GHM= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com