

解:
(1)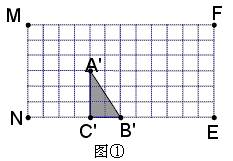
(2)能。如方格纸②所示。设Rt△ABC向右平移t秒,
则NC=t ,BE=10-t,AH=12-t 。
在Rt△ABC中,由勾股定理得: AB2=CB2+CA2=22+32=13 。
同理可得: BF2=BE2+EF2=(10-t)2+62
AF2=AH2+FH2=32+(12-t)2
当AB2+BF2=AF2时,由勾股定理的逆定理得,∠ABF=90°
即△ABF为Rt△。此时由AB2+BF2=AF2
得13+(10-t)2+62=32+(12-t)2 解得t=1。
当AB2+AF2=BF2时,由勾股定理的逆定理得:∠BAF=90°
即△ABF为Rt△。此时由AB2+AF2=BF2
得13+32+(12-t)2 = (10-t)2+62 。解得t=7.5
(3)依题意得:当t=7.5时, 直线AF与Rt△ABC的外接圆相切;
当0<t<7.5或7.5<t<10时,直线AF与Rt△ABC的外接圆相交;
当t=1时, 直线BF与Rt△ABC的外接圆相切;
当0<t<1或1<t<10时,直线BF与Rt△ABC的外接圆相交。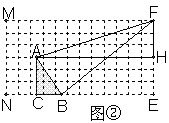


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 4 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,则下列说法中正确的有( )
如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,则下列说法中正确的有( ) 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com