
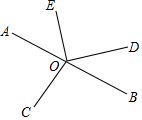
 如图,点O在直线AB上,OC是∠AOB的平分线,在直线AB的另一侧以点O为顶点作∠DOE=90°
如图,点O在直线AB上,OC是∠AOB的平分线,在直线AB的另一侧以点O为顶点作∠DOE=90°分析 (1)由条件可知∠AOE+∠BOD=90°,可求得答案;
(2)由(1)的结论,结合条件可知2∠DOB=90°+∠AOE,可求得∠AOE.
解答 解:
(1)∵点O在直线AB上,
∴∠AOE+∠EOD+∠BOD=180°,
∴∠AOE+∠BOD=180°-90°=90°,
若∠AOE=46°,则∠BOD=90°-46°=44°;
(2)∵OC是∠AOB的平分线,
∴∠COA=90°,
∴∠COE=∠COA+∠AOE,
∵∠COE=2∠DOB,
∴2∠DOB=90°+∠AOE,
由(1)可知∠DOB+∠AOE=90°,
∴∠DOB=90°-∠AOE,
∴2(90°-∠AOE)=90°+∠AOE,
解得∠AOE=30°.
点评 本题主要考查角平分线的定义,掌握角平分线分已知角为两个相等的角是解题的关键,注意方程思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,1) | D. | ( 4,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y2>y1 | D. | y1>y3>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
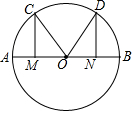 如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:$\widehat{AC}$=$\widehat{BD}$.
如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:$\widehat{AC}$=$\widehat{BD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠BAC=∠BEF=90°,AB=AC=3,EB=EF,BF=1,O为FC的中点,当△EBF绕点B旋转(在△ABC所在平面内)时,AO的最大值为$\frac{3\sqrt{2}+1}{2}$.
如图,∠BAC=∠BEF=90°,AB=AC=3,EB=EF,BF=1,O为FC的中点,当△EBF绕点B旋转(在△ABC所在平面内)时,AO的最大值为$\frac{3\sqrt{2}+1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com