
| 销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
| 月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
分析 (1)设y=kx+b,待定系数法求解即可得;
(2)根据:“总利润=每千克利润×销售量”列出函数关系式,配方可得其最值情况;
(3)由(2)知,第二个月利润需达到1700+550即W=2250才能满足题目条件,解方程可得x的值,根据二次函数性质可得x的取值范围.
解答 解:(1)设y=kx+b,
将(70,100),(75,90)代入上式,
得:$\left\{\begin{array}{l}70k+b=100\\ 75k+b=90\end{array}\right.$
解得:$\left\{\begin{array}{l}k=-2\\ b=240\end{array}\right.$,
则y=-2x+240,
(2)w=(x-50)y
=(x-50)(-2x+240)
=-2x2+340x-9000
=-2(x-85)2+2450,
当x=85时,w最大=2450;
(3)由(2)知,第1个月还有3000-2450=550元的投资成本没有收回.
则要想在全部收投资的基础上使第二个月的利润达到1700元,
即w=2250才可以,
可得方程:-2(x-85)2+2450=2250
解得:x1=75,x2=95
根据题意x2=95不合题意,应舍去,
当x=80时,y=2400,
∵-2<0,
∴当x<85时,w随x的增大而增大,
当w≥2250,且销售单价不高于80时,75≤x≤80.
答:当销售单价为75≤x≤80元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
点评 本题主要考查二次函数的实际应用能力及待定系数求一次函数解析式,根据题意准确抓住相等关系列出函数关系式是解题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )| A. | 20 | B. | 22 | C. | 14 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{2}{3}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{9}{4}$ | D. | $-\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
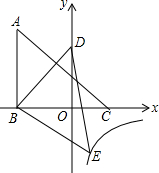 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com