
����Ŀ����ͼ��AB��4������P��A��������ֱ��AB����ÿ��3����λ���ٶ������˶�������B���������أ��ص�A��ֹͣ�˶�������Q��Pͬʱ��A��������ֱ��AB����ÿ��1����λ���ٶ������˶�����Pֹͣ�˶�ʱ����QҲֹͣ�˶������P���˶�ʱ��Ϊt�룮
![]()
��1����t��1����BP�ij����� ��PQ�ij����� ����
��2������P�ص���Aʱ����BQ�ij���
��3����ֱ��AB��ȡ��C��ʹB���߶�PC���е㣬�ڵ�P�������˶������У��Ƿ����AC��AQ+3�������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��1��4����2��![]() ����3������AC��AQ+3����ʱt��ֵΪ
����3������AC��AQ+3����ʱt��ֵΪ![]() ��
��![]()
��������
��1���������⣬��t��1����AP��3t��AQ��t��������𰸣�
��2����P�ص���Aʱ���ߵ���·��ΪAB��2���������ٶ�3�����ʱ�䣬�ٰ�ʱ��������AQ�������BQ��
��3�����ݵ�P�����˶��ͷ����˶���������������ۣ���t��AC��AQ��ʾ���з������t��ע��۲���õ�t�Ƿ�����P���������˶��Ĺ��ɣ�
�⣺��1��t��1ʱ��AP��3��AQ��1
��BP��AB��AP��1��PQ��AQ+AP��4
�ʴ�Ϊ��1��4
��2������P�ص���Aʱ��t��![]()
��AQ��![]()
��BQ��AB+AQ��4+![]() ��
��![]()
��3������AC��AQ+3
�ٵ�0��t��![]() ʱ����P�����˶�
ʱ����P�����˶�
��B��PC�е�
��BC��PB��AB��AP��4��3t
��AC��AB+BC��4+4��3t��8��3t
��AC��AQ+3������8��3t��t+3
��ã�t��![]()
�ڵ�![]() ��t��
��t��![]() ʱ����P�����˶�
ʱ����P�����˶�
��BC��PB��3t��4
��4+3t��4��t+3
��ã�t��![]()
��������������AC��AQ+3����ʱt��ֵΪ![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ6����B����������A������һ�㣬��A��B�����ľ���Ϊ10������P�ӵ�A��������ÿ��3����λ���ȵ��ٶ������������˶���
![]()
��1�������ϵ�B��ʾ�������� ����
��2���˶�1��ʱ����P��ʾ�������� ����
��3������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ������������˶�������P��Qͬʱ��������
�ٵ���P�˶�������ʱ����P���Q����������ʱ��Ӧ���������Ƕ��٣�
�ڵ���P�˶�������ʱ����P���Q�ľ���Ϊ8����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������![]() ������˵���в���ȷ���ǣ� ��
������˵���в���ȷ���ǣ� ��
A. ͼ���㣨1.-2��
B. ͼ��ֲ��ڵڶ���������
C. x>0ʱ��y��x���������
D. ����A��![]() ��B��
��B��![]() ����ͼ���ϣ���
����ͼ���ϣ���![]() ,��
,��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��3�£�ij�н������ܲ����ڳ������п�չ������������֪ʶ���������������������ȡ�˲���ͬѧ�ijɼ���x��Ϊ�������ܷ�100�֣��������������в�������ͳ��ͼ����
������ͳ�Ʊ�
��� | ���ɼ����飨��λ���֣� | ��Ƶ�� | ��Ƶ�� |
��A | ��80��x��85 | ��50 | ��0.1 |
��B | ��85��x��90 | ��75 | |
��C | ��90��x��95 | ��150 | ��c |
��D | ��95��x��100 | ��a | |
���ϼ� | ��b | 1 |
����������Ϣ����������⣺
��1��ͳ�Ʊ��У�a=_____��b=_____��c=_____��
��2������ͳ��ͼ�У�m��ֵΪ_____����C������Ӧ��Բ�ĽǵĶ�����_____��
��3�����μӱ��ξ�����ͬѧ����5000�ˣ�������Ƴɼ���95�ּ����ϵ�ѧ����Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ӭ�����п��ԣ�Сǿ�Կ���ǰʣ��ʱ������һ�����ţ����Ѽƻ���ϰ��Ҫ���ݵ�ʱ����һ���ı���Ȧ��������ͼ�������֣����������ı���Ȧ����������ĺ�ǡ����5�ı������������˼���λ�ã�������������������
��1��������������м����Ϊa����������ʽ�ļӼ�˵�����еĵ�����
��2����������ĺ���Ϊ150�����ܣ���д���м��Ǹ����������ܣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �ֱ�y�ᡢx ����A��B���㣬������
�ֱ�y�ᡢx ����A��B���㣬������![]() ��A��B����.
��A��B����.
��1������������ߵĽ���ʽ��
��2������ֱx���ֱ��x=t���ڵ�һ����ֱ��AB�ڵ�M��������������ڵ�N.��t ȡ��ֵʱ��MN�����ֵ�����ֵ�Ƕ��٣�
��3������2��������£���A��M��N��DΪ������ƽ���ı��Σ�����ĸ�����D������.
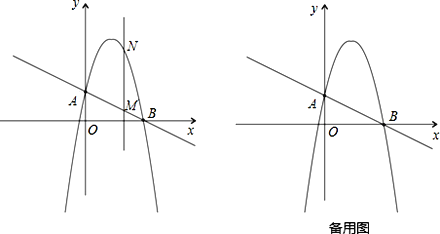
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
��![]() ������
������![]() ����ͼ1��. ��
����ͼ1��. ��![]() �����εıߴӵ�
�����εıߴӵ�![]() �ƶ������
�ƶ������![]() �ƶ��ľ���Ϊ
�ƶ��ľ���Ϊ![]() ��
��![]() .
.
��1����֤��![]() ��
��
��2������![]() �ӵ�
�ӵ�![]() �ƶ�����
�ƶ�����![]() ʱ��
ʱ��![]() ��
��![]() �ĺ�����ϵ����ͼ2���е�����
�ĺ�����ϵ����ͼ2���е�����![]() ��ʾ. ����
��ʾ. ����![]() �ij���
�ij���
��3���ڣ�2��������£���![]() �ӵ�
�ӵ�![]() �ƶ��Ĺ����У�
�ƶ��Ĺ����У�![]() �Ƿ����Ϊ���������Σ����ܣ������������ʹ
�Ƿ����Ϊ���������Σ����ܣ������������ʹ![]() Ϊ���������ε�
Ϊ���������ε�![]() ��ȡֵ�������ܣ���˵������.
��ȡֵ�������ܣ���˵������.
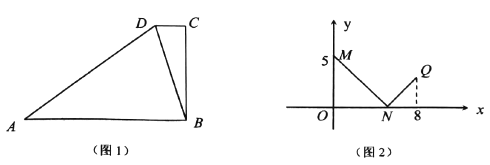
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ı���ABCD�ǡ�O���ڽ��ı���,AB=CD.
(1)��ͼ(1),��֤:AD��BC��
(2)��ͼ(2),��F��AC���е�,��DG��AB,��BC�ڵ�E,��AC�ڵ�M,��֤:AE=2DF��
(3)��(2)��������,��DGƽ�֡�ADC,GE=5![]() ,tan��ADF=4
,tan��ADF=4![]() ,���O�İ뾶��
,���O�İ뾶��
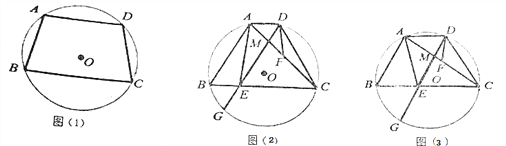
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC��65�㣮��һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����
��1����ͼ���������ǰ�MON��һ��ON������OB�غ�ʱ�����MOC���� ����
��2����ͼ���������ǰ�MON�Ƶ�O��ʱ����תһ���Ƕȣ���ʱOC�ǡ�MOB�Ľ�ƽ���ߣ�����ת�ǡ�BON���� ������CON���� ����
��3������BOC��������NOC�����������ǰ�MON�Ƶ�O��ʱ����ת��ͼ��ʱ�����AOM��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com