
如图, 已知在平面直角坐标系中,一次函数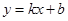 (k≠0)的图象与反比例函数
(k≠0)的图象与反比例函数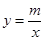 (m≠0)的图象相交于A、B两点,且点B的纵坐标为
(m≠0)的图象相交于A、B两点,且点B的纵坐标为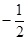 ,过点A作AC⊥x轴于点C, AC=1,OC=2.
,过点A作AC⊥x轴于点C, AC=1,OC=2.
求:(1)求反比例函数和一次函数的关系式;
(2)直接写出反比例函数值大于一次函数值时x的取值范围.
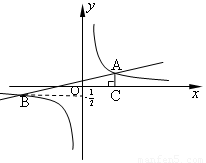
解:(1)∵AC=1,OC=2,且点A在第一象限
∴点A的坐标为(2,1)
∵点A在反比例函数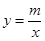 (m≠0)的图象上,∴
(m≠0)的图象上,∴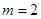
∴反比例函数关系式为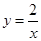 ---------------------------------------------------3分
---------------------------------------------------3分
∵点B在反比例函数图象上,且点B的纵坐标为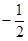
∴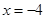 即点B的坐标为(
即点B的坐标为(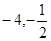 )
)
∵A、B两点均在直线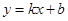 上
上
∴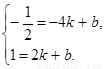 ∴
∴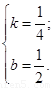
∴一次函数的关系式是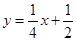 ----------------------------------------------6分
----------------------------------------------6分
(2)当反比例函数值大于一次函数值时,则x的取值范围是
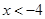 或
或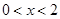 ------------------------------------------10分
------------------------------------------10分
【解析】(1)首先根据已知条件确定点A的坐标为,然后代入反比例函数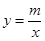 (m≠0)确定m的值,接着求出点B的纵坐标,再利用待定系数法即可求出一次函数的关系式;
(m≠0)确定m的值,接着求出点B的纵坐标,再利用待定系数法即可求出一次函数的关系式;
(2)根据(1)中的函数关系式结合图象即可写出反比例函数值大于一次函数值时x的取值范围.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,直y=
如图,在平面直角坐标系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
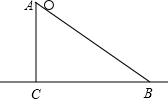
 (2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=
(2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=| 3 |
| 5 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
 在地面上有一个斜坡装置(如图),已知斜坡的铅直高度AC=0.6m,水平距离BC=0.8m,小球从顶端A由静止自由下滑,速度均匀增大,0.2s滑至底端B后,继续在平地上滑行15米停止.
在地面上有一个斜坡装置(如图),已知斜坡的铅直高度AC=0.6m,水平距离BC=0.8m,小球从顶端A由静止自由下滑,速度均匀增大,0.2s滑至底端B后,继续在平地上滑行15米停止.查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第19-26期 总第175-182期 北师大版 题型:022
如图,已知甲运动方式为:先竖直向上运动
1个单位长度,再水平向右移动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度,再水平向左移动3个单位长度.在平面直角坐标系内,现有一动点P,第一次从原点O出发按甲方式运动到点P1,第二次从点P1出发按乙方式运动到点P2,第三次从点P2出发再按甲方式运动到点P3,第四次从点P3出发在按乙方式运动到P4,…依此运动规律,则经过第11次运动后,动点P所在位置P11的坐标是________.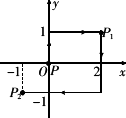
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com