
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

【答案】(1)见解析 (2)![]()
【解析】(1)延长EB交DG于点H,先证出Rt△ADG≌Rt△ABE,得出∠AGD=∠AEB,﹢根据∠HBG=∠EBA,得出∠HGB+∠HBG=90°即可;
(2)过点A作AP⊥BD交BD于点P,根据△DAG≌△BAE得出DG=BE,∠APD=90°,求出AP、DP,利用勾股定理求出PG,﹢根据DG=DP+PG求出DG,最后根据DG=BE即可得出答案.
解:(1)如解图①所示,延长EB交DG于点H.
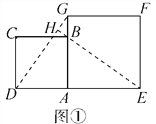
∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE,
∴△ADG≌△ABE(SAS), ∴∠AGD=∠AEB.
在△ADG中,∠AGD+∠ADG=90°,
∴∠AEB+∠ADG=90°.
在△EDH中,∠AEB+∠ADG+∠DHE=180°,
∴∠DHE=90°,即DG⊥BE
(2)如解图②,连结DG,过点A作AM⊥DG交DG于点M,
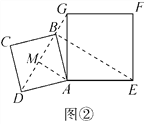
∠AMD=∠AMG=90°.
∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAB=∠GAE=90°,AG=AE,
∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE.
在△ADG和△ABE中,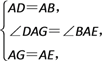
∴△ADG≌△ABE(SAS),∴DG=BE.
∵BD为正方形ABCD的对角线,∴∠MDA=45°.
在Rt△AMD中,∠MDA=45°,
∵AD=2,∴DM=AM=![]() ,
,
在Rt△AMG中,根据勾股定理得:
GM=![]() =
=![]() .
.
∵DG=DM+GM=![]() +
+![]() ,
,
∴BE=DG=![]() +
+![]()


科目:初中数学 来源: 题型:
【题目】下列乘法中,不能运用平方差公式进行运算的是( )
A.(x+a)(x-a)B.(b+m)(m-b)C.(-x-b)(x-b)D.(a+b)(-a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园把一筐桔子分给若干个小朋友,若每人3只,那么还剩59只,若每人5只,那么最后一个小朋友分到桔子,但不足4只,试求这筐桔子共有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
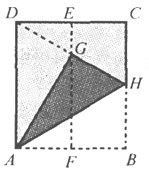
A. 2cm B. ![]() cm C. 4cm D.
cm C. 4cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做了如下四个因式分解题,你认为小明做得不完整一题是( )
A. x2y﹣xy2=xy(x﹣y) B. m2﹣2mn+n2=(m﹣n)2
C. a3﹣a=a(a2﹣1) D. ﹣x2+y2=(y+x)(y﹣x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com